
【题目】下列命题中,判断条件p是条件q的什么条件:
(1)p:|x|=|y|,q:x=y;
(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;
(3)p:四边形的对角线互相平分,q:四边形是矩形.
【答案】
(1)
【解答】∵|x|=|y| ![]() x=y,但x=y|x|=|y|,
x=y,但x=y|x|=|y|,
∴p是q的必要条件,但不是充分条件.
(2)
【解答】
△ABC是直角三角形![]() △ABC是等腰三角形.
△ABC是等腰三角形.
△ABC是等腰三角形![]() △ABC是直角三角形.∴p既不是q的充分条件,也不是q的必要条件.
△ABC是直角三角形.∴p既不是q的充分条件,也不是q的必要条件.
(3)
【解答】四边形的对角线互相平分四边形是矩形.四边形是矩形四边形的对角线互相平分.∴p是q的必要条件,但不是充分条件.
【解析】解答此类问题的关键是分析条件p和q是否具有推出关系,首先要化简条件,其次要明确条件p是什么,结论q是什么,接着判断一是p能否推得条件q;二是q能否推得条件p , 方可解决;注意养成“解决彻底”的好习惯,既要解决充分性,又要解决必要性.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的不等式ax>1(a>0,a≠1)的解集是{x|x<0},命题q:函数y=lg(ax2-x+a)的定义域为R,如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2017年上半年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
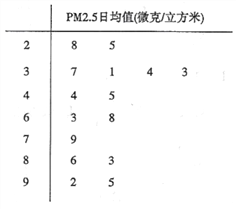
(1)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(2)从这15天的数据中任取3天的数据,记![]() 表示其中空气质量达到一级的天数,求
表示其中空气质量达到一级的天数,求![]() 的分布列;
的分布列;
(3)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y)+ ![]() ,且f(
,且f( ![]() )=0,当x>
)=0,当x> ![]() 时,f(x)>0.
时,f(x)>0.
(1)求f(1);
(2)判断函数f(x)的单调性,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
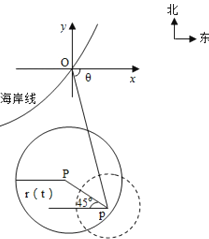
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南![]() 方向
方向![]() 的海面P处,且
的海面P处,且![]() ,并以
,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移动,台风侵袭的范围为圆形区域,当前半径为
方向移动,台风侵袭的范围为圆形区域,当前半径为![]() ,并以
,并以![]() 的速度不断增大,问几小时后该城市开始受到台风的侵袭?
的速度不断增大,问几小时后该城市开始受到台风的侵袭?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com