
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD 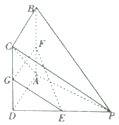
(1)证明AC⊥PB
(2)证明:平面PBC∥平面EFG.
【答案】
(1)证明:连结BD,
∵PD⊥平面ABCD,∴PD⊥AC,
∵底面ABCD是正方形,∴BD⊥AC,
又PD∩BD=D,∴AC⊥平面PBD,
∵PB平面PBD,∴AC⊥PB
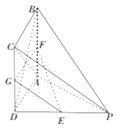
(2)证明:∵G、E分别为CD、PD的中点,∴CE∥PC,
又GE平面PBC,PC平面PBC,
∴GE∥平面PBC,
在正方形ABCD中,G、F分别为CD、AB的中点,
∴GF∥BC,又GF平面PBC,BC平面PBC,
∴GF∥平面PBC,
∵GF∩GE=G,∴平面PBC∥平面EFG
【解析】(1)连结BD,推导出PD⊥AC,BD⊥AC,从而AC⊥平面PBD,由此能证明AC⊥PB.(2)推导出GE∥平面PBC,GF∥平面PBC,由此能证明平面PBC∥平面EFG.
【考点精析】利用空间中直线与直线之间的位置关系和平面与平面平行的判定对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+ax﹣2a2+3a)ex(x∈R),其中a∈R.
(1)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当 ![]() 时,求函数f(x)的单调区间和极值.
时,求函数f(x)的单调区间和极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
⑴ 若曲线![]() 在点
在点![]() 处的切线经过点
处的切线经过点![]() ,求实数
,求实数![]() 的值;
的值;
⑵ 若函数![]() 在区间
在区间![]() 上单调,求实数
上单调,求实数![]() 的取值范围;
的取值范围;
⑶ 设![]() ,若对
,若对![]() ,
, ![]() ,使得
,使得![]() 成立,求整数
成立,求整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f(
的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f( ![]() )=
)= ![]() .
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(﹣1,1)上是增函数;
(3)解不等式f(x2﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设入射光线沿直线y=2x+1射向直线y=x,则被y=x反射后,反射光线所在的直线方程是( )
A.x﹣2y﹣1=0
B.x﹣2y+1=0
C.3x﹣2y+1=0
D.x+2y+3=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x2﹣2ax+3).
(x2﹣2ax+3).
(1)若f(x)的定义域为R,求a的取值范围;
(2)若f(﹣1)=﹣3,求f(x)单调区间;
(3)是否存在实数a,使f(x)在(﹣∞,2)上为增函数?若存在,求出a的范围?若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com