
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,AP=AB=AC=a, ![]() ,PA⊥底面ABCD.
,PA⊥底面ABCD. 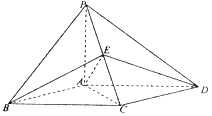
(1)求证:平面PCD⊥平面PAC;
(2)在棱PC上是否存在一点E,使得二面角B﹣AE﹣D的平面角的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值?若不存在,说明理由.
的值?若不存在,说明理由.
【答案】
(1)证明:在△ACD中,AC=a,CD=a,AD= ![]() a,
a,
由勾股定理得:CD⊥AC
∵PA⊥底面ABCD,∴PA⊥CD,
AC面PAC,PA面PAC,PA∩AC=A
∴CD⊥面PAC
又∵CD面PCD
∴平面PCD⊥平面PAC
(2)解:(由(1)知:AB⊥AC,又PA⊥底面ABCD
∴以A为原点,AB,AC,AP所在直线分别为x轴,y轴,z轴建立如图所示坐标系
则A(0,0,0),B(a,0,0),C(0,a,0),
D(﹣a,a,0),P(0,0,a)
假设点E存在,且λ= ![]() ,则
,则 ![]() =λ
=λ ![]() (xE,yE﹣a,zE)=λ(0,﹣a,a)
(xE,yE﹣a,zE)=λ(0,﹣a,a)
∴xE=0,yE=(1﹣λ)a,zE=λa
![]() =(a,0,0)
=(a,0,0) ![]() =(0,(1﹣λ)a,λa),
=(0,(1﹣λ)a,λa), ![]() =(﹣a,a,0)
=(﹣a,a,0)
设平面BAE的法向量为 ![]() =(x1,y1,z1),平面DAE的法向量为
=(x1,y1,z1),平面DAE的法向量为 ![]() =(x2,y2,z2),
=(x2,y2,z2),
则  ,取y1=λ,得
,取y1=λ,得 ![]() ,
,
 ,取x2=λ,得
,取x2=λ,得 ![]() =(λ,λ,λ﹣1)
=(λ,λ,λ﹣1)
cos< ![]() >=
>=  =
= ![]() =
= ![]() ,
,
由题意:|cos< ![]() >|=
>|= ![]() =
= ![]() ,
,
整理得:3(2λ2﹣2λ+1)=2(3λ2﹣2λ+1),解得λ= ![]() ,
,
∴棱PC上存在一点E,使得二面角B﹣AE﹣D的平面角的余弦值为﹣ ![]() ,且此时λ=
,且此时λ= ![]() .
.

【解析】(1)由勾股定理得:CD⊥AC,由线面垂直得PA⊥CD,从而CD⊥面PAC,由此能证明平面PCD⊥平面PAC.(2)以A为原点,AB,AC,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出结果.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】设数列{an}是集合{x|x=3s+3t , s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为 . 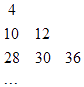
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1,在△ABC中,内角A,B,C的对边分别为a,b,c,且f(B)=1.
sinxcosx+2cos2x﹣1,在△ABC中,内角A,B,C的对边分别为a,b,c,且f(B)=1.
(1)求B;
(2)若 ![]()
![]() =3,求b的取值范围.
=3,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求职”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完成等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,即S= ![]() ,现有周长为10+2
,现有周长为10+2 ![]() 的△ABC满足sinA:sinB:sinC=2:3:
的△ABC满足sinA:sinB:sinC=2:3: ![]() ,则用以上给出的公式求得△ABC的面积为( )
,则用以上给出的公式求得△ABC的面积为( )
A.![]()
B.![]()
C.![]()
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 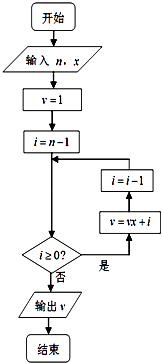
A.20
B.61
C.183
D.548
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣ax+lnx,a∈R.
(1)当a=3时,求函数f(x)的极小值;
(2)令g(x)=x2﹣f(x),是否存在实数a,当x∈[1,e](e是自然对数的底数)时,函数g(x)取得最小值为1.若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为1的单调递增的等比数列,且满足a3 , ![]() 成等差数列.
成等差数列.
(1)求{an}的通项公式;
(2)若bn=log3(anan+1)(n∈N*),求数列{anbn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com