练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知,定点,定直线和上的动点满足：在直线的同侧,点在直线的另一侧.以为焦点作与直线相切的椭圆,且当在上运动时,椭圆的长轴长为定值.

    (1)求直线的方程；

    (2)对于第一象限内任意2012个在椭圆上的点,是否一定可以将它们分成两组,使得其中一组点的横坐标之和不大于2013,另一组点的纵坐标之和不大于2013?请证明你的结论.

    【答案】（1）（2）见解析

    【解析】

    (1)设点关于直线的对称点为.则过椭圆与直线的切点.从而, (即椭圆的长轴长)为定值.于是,点Q在以为圆心、为半径的圆上.

    由的任意性及在上,知.故点与重合,即直线为线段的中垂线.

    注意到,.

    因为的中点为,所以,直线的方程为.

    (2)可以.

    设这2012个点为.

    由(1)知直线的方程为.

    又易知点在直线的下方,故,且.

    不失一般性,不妨设.

    (i)若,则将点分为一组,点作为一组符合题意.

    (ii)若,则存在,使得

    ,且.

    于是,对任意的,有.

    故

    将点分为一组,点分为一组.则前一组点的横坐标之和不大于2013,后一组点的纵坐标之和不大于2013.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系中，直线的参数方程是（为参数)，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为．将曲线上每一点的横坐标伸长到原来的两倍（纵坐标不变）得到曲线．

    （1）求曲线的直角坐标方程；

    （2）已知点，若直线与曲线交于，两点，且，求直线的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，讨论极值点的个数；

    （2）若函数有两个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设外接圆上三段弧的中点依次为,其关于的对称点依次为.若顶点与对应旁切圆切点的连线交于一点 (界心),为的垂心，证明：在以为直径的圆上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2－mlnx，h(x)＝x2－x＋a.

    (1)当a＝0时，f(x)≥h(x)在(1，＋∞)上恒成立，求实数m的取值范围；

    (2)当m＝2时，若函数k(x)＝f(x)－h(x)在区间(1,3)上恰有两个不同零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某次会操活动中，领操员让编号为的名学生排成一个圆形阵，做循环报数，领操员一一记录报数者的编号，并要求报l、2的学生出列，报3的学生留在队列中，并将编号改为此次循环报数中三名学生的编号之和．一直循环报数下去．当操场上剩余的学生人数不超过两名时，报数活动结束．领操员记录最后留在操场的学生编号（例如，编号为的九名学生排成一个圆形阵，报数结束后，只有原始编号为9的学生留在操场，此时，他的编号为45，领操员记录下来的数据分别为l，2，3，4，5，6，7，8，9，6，15，24，45）．已知共有2011名学生参加会操．

    （1）最后留在场内的学生最初的编号是几号?

    （2）求领操员记录下的编号之和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为抗击新冠病毒，某部门安排甲、乙、丙、丁、戊五名专家到三地指导防疫工作.因工作需要，每地至少需安排一名专家，其中甲、乙两名专家必须安排在同一地工作，丙、丁两名专家不能安排在同一地工作，则不同的分配方法总数为（ ）

    A.18B.24C.30D.36

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2022年北京冬奥运动会即第24届冬季奥林匹克运动会将在2022年2月4日至2月20日在北京和张家口举行，某研究机构为了了解大学生对冰壶运动的兴趣，随机从某大学生中抽取了120人进行调查，经统计男生与女生的人数比为11:13，男生中有30人表示对冰壶运动有兴趣，女生中有15人对冰壶运动没有兴趣.

    （1）完成列联表，并判断能否有99%的把握认为“对冰壶运动是否有兴趣与性别有关”？

    有兴趣

    没有兴趣

    合计

    男

    30

    女

    15

    合计

    120

    （2）用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取8人，求抽取的男生和女生分别为多少人？若从这8人中选取两人作为冰壶运动的宣传员，求选取的2人中恰好有1位男生和1位女生的概率.

    附:，其中n=a+b+c+d

    P

    0.150

    0.100

    0.050

    0.025

    0.010

    2.072

    2.076

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某知名电商在双十一购物狂欢节中成交额再创新高，月日单日成交额达亿元.某店主在此次购物狂欢节期间开展了促销活动，为了解买家对此次促销活动的满意情况，随机抽取了参与活动的位买家，调查了他们的年龄层次和购物满意情况，得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图：

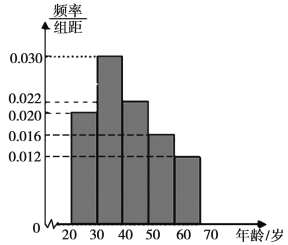
    “购物评价为满意”的年龄层次频数分布表：

    年龄（岁）

    频数

    （1）估计参与此次活动的买家的平均年龄（同一组中的数据用该组区间的中点值做代表）；

    （2）若年龄在岁以下的称为“青年买家”，年龄在岁以上（含岁）的称为“中年买家”，完成下面的列联表，并判断能否有的把握认为中、青年买家对此次活动的评价有差异？

    评价满意

    评价不满意

    合计

    中年买家

    青年买家

    合计

    附：参考公式：.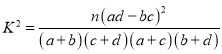

    查看答案和解析>>

    同步练习册答案