
 (m∈Z),则m叫做离实数x最近的整数,记作{x},即{x}=m;在此基础上有函数f(x)=|x-{x}|(x∈R).对于函数f(x)给出如下判断:①函数f(x)是偶函数;②函数f(x)是周期函数;③函数f(x)在区间
(m∈Z),则m叫做离实数x最近的整数,记作{x},即{x}=m;在此基础上有函数f(x)=|x-{x}|(x∈R).对于函数f(x)给出如下判断:①函数f(x)是偶函数;②函数f(x)是周期函数;③函数f(x)在区间 上单调递增;④函数f(x)的图象关于直线
上单调递增;④函数f(x)的图象关于直线 (k∈Z)对称.则以上判断中正确结论的个数是( )
(k∈Z)对称.则以上判断中正确结论的个数是( )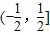 上不是单调递增.④利用若函数满足f(a-x)=f(x),则函数对称轴为x=
上不是单调递增.④利用若函数满足f(a-x)=f(x),则函数对称轴为x=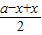 ,来判断函数的对称性.
,来判断函数的对称性.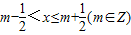 ,
,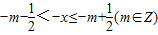
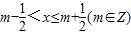 ,∴
,∴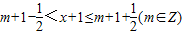
 ∈
∈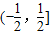 ,
, ∈
∈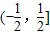 ,且{
,且{ }=0,{
}=0,{ }=0
}=0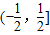 上单调递增,∴③错误
上单调递增,∴③错误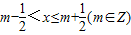 ,∴
,∴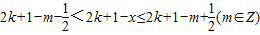
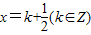 对称
对称

科目:高中数学 来源:天津市新人教A版数学2012届高三单元测试2:命题及其关系 题型:022
给出定义:若![]() (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
①函数y=f(x)的定义域是R,值域是[0,![]() ];
];
②函数y=f(x)的图像关于直线x=![]() (k∈Z)对称;
(k∈Z)对称;
③函数y=f(x)是周期函数,最小正周期是1;
④函数y=f(x)在![]() 上是增函数;
上是增函数;
则其中真命题是_________.
查看答案和解析>>
科目:高中数学 来源:湖南省长沙市雅礼中学2009届高三第七次月考数学理科试题 题型:013
给出定义:若![]() (其中m为整数),则m叫做离实数x最近的整数,记作{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
(其中m为整数),则m叫做离实数x最近的整数,记作{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
①函数y=f(x)的定义域为R,值域为![]() ;
;
②函数y=f(x)的图像关于直线![]() (k∈Z)对称;
(k∈Z)对称;
③函数y=f(x)是周期函数,最小正周期为1;
④函数y=f(x)在![]() 上是增函数.
上是增函数.
其中正确的命题个数为
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
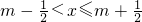 (m∈Z),则称m为离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=|x-{x}|的五个命题:
(m∈Z),则称m为离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=|x-{x}|的五个命题: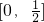 ;
; 上是增函数;
上是增函数;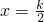 (k∈Z)对称;
(k∈Z)对称;查看答案和解析>>
科目:高中数学 来源: 题型:单选题
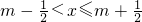 (m∈Z),则m叫做离实数x最近的整数,记作{x},即{x}=m;在此基础上有函数f(x)=|x-{x}|(x∈R).对于函数f(x)给出如下判断:①函数f(x)是偶函数;②函数f(x)是周期函数;③函数f(x)在区间
(m∈Z),则m叫做离实数x最近的整数,记作{x},即{x}=m;在此基础上有函数f(x)=|x-{x}|(x∈R).对于函数f(x)给出如下判断:①函数f(x)是偶函数;②函数f(x)是周期函数;③函数f(x)在区间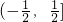 上单调递增;④函数f(x)的图象关于直线
上单调递增;④函数f(x)的图象关于直线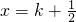 (k∈Z)对称.则以上判断中正确结论的个数是
(k∈Z)对称.则以上判断中正确结论的个数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com