
 已知甲、乙两个工厂在今年的1月份的利润都是6万元,且甲厂在2月份的利润是14万元,乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型:f(x)=a1x2+b1x+6,g(x)=a2•3x+b2,(a1,a2,b1,b2∈R).
已知甲、乙两个工厂在今年的1月份的利润都是6万元,且甲厂在2月份的利润是14万元,乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型:f(x)=a1x2+b1x+6,g(x)=a2•3x+b2,(a1,a2,b1,b2∈R).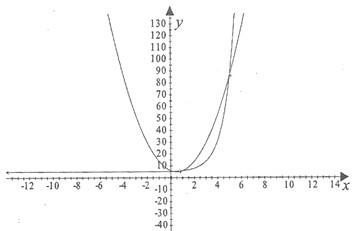 解:(1)依题意:由
解:(1)依题意:由
|
|
|
|
| 1 |
| 3 |
| 1 |
| 3 |


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
 已知甲、乙两个工厂在今年的1月份的利润都是6万元,且甲厂在2月份的利润是14万元,乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份之间的函数关系式分别符合下列函数模型:f(x)=a1x2+b1x+6,g(x)=a2•3x+b2,(a1,a2,b1,b2∈R)
已知甲、乙两个工厂在今年的1月份的利润都是6万元,且甲厂在2月份的利润是14万元,乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份之间的函数关系式分别符合下列函数模型:f(x)=a1x2+b1x+6,g(x)=a2•3x+b2,(a1,a2,b1,b2∈R)查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高一上学期期末模拟数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知甲、乙两个工厂在今年的1月份的利润都是6万,且乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型:f(x)=a1x2—4x+6,g(x)=a2 +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R).
(1)求函数f(x)与g(x)的解析式;
(2)求甲、乙两个工厂今年5月份的利润;
(3)在同一直角坐标系下画出函数f(x)与g(x)的草图,并根据草图比较今年1—10月份甲、乙两个工厂的利润的大小情况.
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高一上学期期末考试数学试卷 题型:解答题
已知甲、乙两个工厂在今年的1月份的利润都是6万元,且甲厂在2月份的利润是14万元,乙厂在2月份的利润是8万元。若甲、乙两个工厂的利润(万元)与月份 之间的函数关系式分别符合下列函数模型:
之间的函数关系式分别符合下列函数模型: ,
, ,
, .
.
(1)求甲、乙两个工厂今年5月份的利润;
(2)在同一直角坐标系下画出函数 与
与 的草图,并根据草图比较今年甲、乙两个工厂的利润的大小情况.
的草图,并根据草图比较今年甲、乙两个工厂的利润的大小情况.

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com