
【题目】
已知椭圆![]() 的右焦点为
的右焦点为![]() ,以椭圆
,以椭圆![]() 与双曲线
与双曲线![]() 两条渐近线的四个交点为顶点的四边形的面积为
两条渐近线的四个交点为顶点的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 为椭圆
为椭圆![]() 上的两点(
上的两点(![]() 不同时在
不同时在![]() 轴上),点
轴上),点![]() ,证明:存在实数
,证明:存在实数![]() ,当
,当![]() 三点共线时,
三点共线时,![]() 为常数.
为常数.
科目:高中数学 来源: 题型:
【题目】将函数y=f(x)的图象向右平移 ![]() 单位得到函数y=cos2x的图象,则f(x)=( )
单位得到函数y=cos2x的图象,则f(x)=( )
A.﹣sin2x
B.cos2x
C.sin2x
D.﹣cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
(1)分别求出m,n的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s ![]() 和s
和s ![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率. 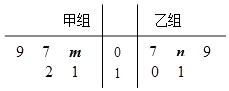
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在的安卓手机盛行一款“心有灵犀”的猜数字游戏,具体的规则如下:
玩家随机输入0~5中的三位数字(数字不重复),按“OK”键确定答案是否正确,手机会给出“xAyB”的提示,其中“xA”表示你输入的三位数字中,有“x”个数字和位置都与答案相同,其中“yB”表示你输入的三位数字中,有“y”个数字与答案相同,但是位置不同,例如:答案为“012”,当你输入“132”时会显示:“1A1B”.
(1)当你第一次输入时,手机显示“1A1B”的概率为多少?
(2)当你第一次输入时,且手机显示“xA2B”时,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
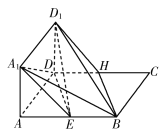
如图所示,正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() .
.
(1)若点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是不在抛物线上的一个动点,过点
是不在抛物线上的一个动点,过点![]() 向抛物线
向抛物线![]() 作两条切线
作两条切线![]() ,切点分别为
,切点分别为![]() .
.
(1)如果点![]() 在直线
在直线![]() 上,求
上,求![]() 的值;
的值;
(2)若点![]() 在以
在以![]() 为圆心,半径为4的圆上,求
为圆心,半径为4的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数f(x)满足:
①对任意x,y∈R,都有:f(x+y)=f(x)+f(y)﹣1;
②当x<0时,f(x)>1.
(Ⅰ)试判断函数f(x)﹣1的奇偶性;
(Ⅱ)试判断函数f(x)的单调性;
(Ⅲ)若不等式f(a2﹣2a﹣7)+ ![]() >0的解集为{a|﹣2<a<4},求f(5)的值.
>0的解集为{a|﹣2<a<4},求f(5)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com