
(10分)为了预防流感,某学校对教室用药熏消毒法进行消毒。已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为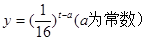 ,如图所示。
,如图所示。
(1)请写出从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室。那么,从药物释放开始,至少需要经过多少小时后,学生才能回到教室。
科目:高中数学 来源: 题型:解答题
已知函数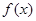 是定义在
是定义在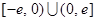 上的奇函数,当
上的奇函数,当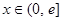 时,有
时,有 (其中
(其中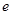 为自然对数的底,
为自然对数的底,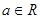 ).
).
(1)求函数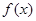 的解析式;
的解析式;
(2)设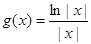 ,
,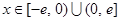 ,求证:当
,求证:当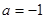 时,
时,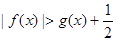 ;
;
(3)试问:是否存在实数 ,使得当
,使得当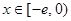 时,
时,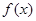 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数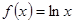 ,
,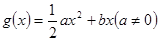
(1)若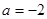 时,
时,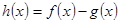 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围;
(2)设函数 的图象
的图象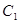 与函数
与函数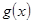 的图象
的图象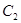 交于
交于 ,
,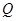 两点,过线段
两点,过线段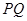 的中点
的中点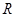 作
作 轴的垂线分别交
轴的垂线分别交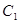 、
、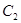 于点
于点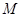 ,
,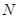 ,问是否存在点
,问是否存在点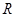 ,使
,使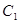 在
在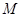 处的切线与
处的切线与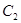 在
在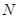 处的切线平行?若存在,求
处的切线平行?若存在,求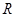 的横坐标,若不存在,请说明理由。
的横坐标,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).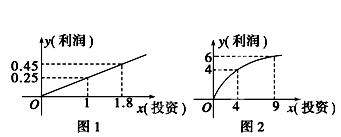
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)某工厂有214名工人, 现要生产1500件产品, 每件产品由3个A型零件与1个B型零件配套组成, 每个工人加工5个A型零件与3个B型零件所需时间相同. 现将全部工人分为两组, 分别加工一种零件, 同时开始加工. 设加工A型零件的工人有x人, 在单位时间内每人加工A型零件5k个(k∈N*), 加工完A型零件所需时间为g(x), 加工完B型零件所需时间为h (x).
(Ⅰ) 试比较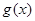 与
与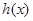 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间 的表达式;
的表达式;
(Ⅱ) 怎样分组才能使完成任务所需时间最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: ,其中
,其中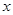 是仪器的月产量
是仪器的月产量
(1)将利润 表示为月产量
表示为月产量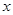 的函数
的函数
(2)当月产量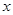 为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com