
(1)求证:四边形EFGH是正方形.
(2)E、F在什么位置时,定制这批地砖所需的材料费用最省?
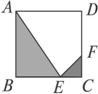
(1)
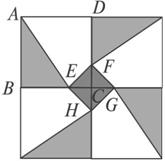
(2)
思路分析:(1)由于四块地砖拼出了四边形EFGH,只需证明△CFE,△CFG,△CGH,△CEH为等腰直角三角形即可;(2)建立数学模型,转化为数学问题.设CE=x,每块地砖的费用为W,求出函数W=f(x)的解析式,转化为讨论求函数的最小值问题.
解:(1)图(2)可以看成是由四块图(1)所示的地砖绕点C按顺时针旋转90°后得到,则有CE=CF,∠ECF=90°,
∴△CFE为等腰直角三角形.
同理,可得△CFG,△CGH,△CEH为等腰直角三角形.
∴四边形EFGH是正方形.
(2)设CE=x,则BE=0.4-x,每块地砖的费用为W,设制成△CFE、△ABE和四边形AEFD三种材料的每平方米价格依次为3a、2a、a(元),
W=![]() x2·3a+
x2·3a+![]() ×0.4×(0.4-x)×2a+[0.16
×0.4×(0.4-x)×2a+[0.16![]() x2
x2![]() ×0.4×(0.4-x)]a
×0.4×(0.4-x)]a
=a(x2-0.2x+0.24)
=a[(x-0.1)2+0.23](0<x<0.4).
由于a>0,则当x=0.1时,W有最小值,即总费用为最省,
即当CE=CF=0.1米时,总费用最省.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
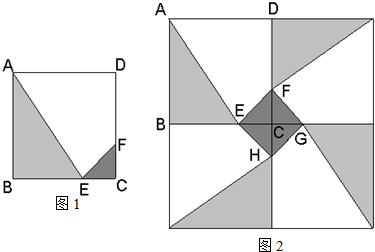
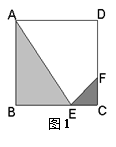
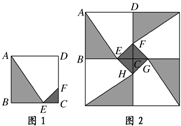 (2007•上海)某人定制了一批地砖.每块地砖 (如图1所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.
(2007•上海)某人定制了一批地砖.每块地砖 (如图1所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.查看答案和解析>>
科目:高中数学 来源: 题型:
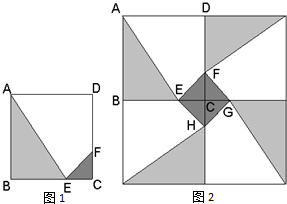 某人定制了一批地砖,每块地砖 (如图1所示)是边长为40cm的正方形ABCD,点E,F分别在边BC和CD上,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形EFGH.则当CE=
某人定制了一批地砖,每块地砖 (如图1所示)是边长为40cm的正方形ABCD,点E,F分别在边BC和CD上,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形EFGH.则当CE=查看答案和解析>>
科目:高中数学 来源: 题型:
某人定制了一批地砖. 每块地砖 (如图1所示)是边长为![]() 米的正方形
米的正方形![]() ,点E、F分别在边BC和CD上, △
,点E、F分别在边BC和CD上, △![]() 、△
、△![]() 和四边形
和四边形![]() 均由单一材料制成,制成△
均由单一材料制成,制成△![]() 、△
、△![]() 和四边形
和四边形![]() 的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形
的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形![]() .
.

(1) 求证:四边形![]() 是正方形;
是正方形;
(2) ![]() 在什么位置时,定制这批地砖所需的材料费用最省?
在什么位置时,定制这批地砖所需的材料费用最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com