
【题目】在数列![]() 中,已知
中,已知![]() ,
,![]() (n∈N*)
(n∈N*)
(1)求数列![]() 的通项公式
的通项公式
(2)若![]() (λ为非零常数),问是否存在整数λ使得对任意n∈N*都有
(λ为非零常数),问是否存在整数λ使得对任意n∈N*都有![]() ?若存在,求出λ的值;若不存在,请说明理由.
?若存在,求出λ的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知,得an=Sn﹣1+3n﹣4(n≥2),利用an与sn的关系,两式相减,an+1+3=2(an+3)(n≥2),初步判断新数列{an+3}具有等比数列的性质,再考虑n=1的情形;
(2)写出数列{bn}的通项,首先假设存在λ使得满足题意,然后计算化简bn+1﹣bn,再结合恒成立问题进行转化,将问题转化为:![]() 对任意的n∈N*恒成立.然后分n为奇偶数讨论即可获得λ的范围,再结合为整数即可获得问题的解答.
对任意的n∈N*恒成立.然后分n为奇偶数讨论即可获得λ的范围,再结合为整数即可获得问题的解答.
(1)由an+1=Sn+3n﹣1(n∈N*)①
得an=Sn﹣1+3n﹣4(n≥2)②
①﹣②得an+1=2an+3(n≥2)
∴an+1+3=2(an+3)(n≥2)
又由②得 a2=S1+6﹣4=a1+2=1
∴a2+3=4
∴a2+3=2(a1+3)
∴an+1+3=2(an+3)(n≥1)
∵a1+3≠0,∴an+3≠0,∴![]()
∴数列{an+3}是首项为2,公比为2的等比数列
∴an+3=2×2n﹣1=2n
∴数列{an}的 an=2n﹣3(n≥1)
(2)由(1)可得 bn=3n+(﹣1)n﹣1λ2n
bn+1=3n+1+(﹣1)nλ2n+1
要使bn+1>bn恒成立,只需bn+1﹣bn=23n﹣3λ(﹣1)n﹣12n>0恒成立,
即![]() 恒成立
恒成立
当n为奇数时,![]() 恒成立 而
恒成立 而![]() 的最小值为1∴λ<1
的最小值为1∴λ<1
当n为偶数时,![]() 恒成立 而
恒成立 而![]() 最大值为
最大值为![]() ∴
∴![]()
即λ的取值范围是1>![]() ,且λ≠1
,且λ≠1
又λ为整数.
∴存在λ=﹣1或0,使得对任意n∈N*都有bn+1>bn.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:

(1)求该班全体男生的人数;
(2)求分数在![]() 之间的男生人数,并计算频率分布直方图中
之间的男生人数,并计算频率分布直方图中![]() 之间的矩形的高.
之间的矩形的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}为等差数列,且a5=14,a7=20,数列{bn}的前n项和为Sn , b1= ![]() 且3Sn=Sn﹣1+2(n≥2,n∈N).
且3Sn=Sn﹣1+2(n≥2,n∈N).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=anbn , n=1,2,3,…,Tn为数列{cn}的前n项和,Tn<m对n∈N*恒成立,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是(﹣1,1)上的偶函数,且在区间(﹣1,0)上是单调递增的,A,B,C是锐角三角形△ABC的三个内角,则下列不等式中一定成立的是( )
A.f(sinA)>f(sinB)
B.f(sinA)>f(cosB)
C.f(cosC)>f(sinB)
D.f(sinC)>f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:
(1)求该班全体男生的人数;
(2)求分数在![]() 之间的男生人数,并计算频率公布直方图中
之间的男生人数,并计算频率公布直方图中![]() 之间的矩形的高;
之间的矩形的高;
(3)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表).

查看答案和解析>>
科目:高中数学 来源: 题型:
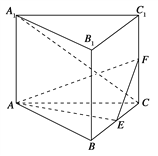
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示程序框图是用“二分法”求方程![]() 的近似解的算法,有下列判断:
的近似解的算法,有下列判断:
①若![]() 则输出的值在
则输出的值在![]() 之间;
之间;
②若![]() 则程序执行完毕将没有值输出;
则程序执行完毕将没有值输出;
③若![]() 则程序框图最下面的判断框刚好执行8次程序就结束.
则程序框图最下面的判断框刚好执行8次程序就结束.
其中正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com