
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的最小值;
的最小值;
(Ⅱ)解不等式![]()
【答案】(1)5;(2)![]() .
.
【解析】试题分析:⑴利用绝对值不等式的性质,求得函数的最小值;
⑵方法一:去掉绝对值,写成分段函数的形式,然后求解;方法二:作出函数的图象,数形结合,解不等式
解析:(Ⅰ)因为f(x)=|2x-1|+2|x+2|≥|(2x-1)-2(x+2)|=5,
所以
(Ⅱ)解法一:f(x)=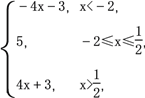
当x<-2时,由-4x-3<8,解得x>-![]() ,即-
,即-![]() <x<-2;
<x<-2;
当-2≤x≤![]() 时,5<8恒成立,即-2≤x≤
时,5<8恒成立,即-2≤x≤![]() ;
;
当x>![]() 时,由4x+3<8,解得x<
时,由4x+3<8,解得x<![]() ,即
,即![]() <x<
<x<![]() ,
,
所以原不等式的解集为![]() .
.
解法二(图象法):f(x)=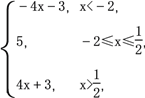
函数f(x)的图象如图所示,

令f(x)=8,解得x=-![]() 或x=
或x=![]() ,
,
所以不等式f(x)<8的解集为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为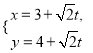 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系
轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系![]() 有相同的长度单位,曲线
有相同的长度单位,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() 两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组: ![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:

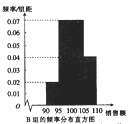
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期;
的分布列及数学期;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
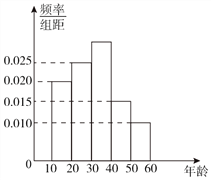
【题目】2017年是内蒙古自治区成立70周年.某市旅游文化局为了庆祝内蒙古自治区成立70周年,举办了第十三届成吉思汗旅游文化周.为了了解该市关注“旅游文化周”居民的年龄段分布,随机抽取了![]() 名年龄在
名年龄在![]() 且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.
且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.
年龄 |
|
|
|
单人促销价格(单位:元) |
|
|
|
(Ⅰ)根据频率分布直方图,估计该市被抽取市民的年龄的平均数;
(Ⅱ)某旅行社针对“旅游文化周”开展不同年龄段的旅游促销活动,各年龄段的促销价位如表所示.已知该旅行社的运营成本为每人![]() 元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
(Ⅲ)若按照分层抽样的方法从年龄在![]() ,
, ![]() 的居民中抽取
的居民中抽取![]() 人进行旅游知识推广,并在知识推广后再抽取
人进行旅游知识推广,并在知识推广后再抽取![]() 人进行反馈,求进行反馈的居民中至少有
人进行反馈,求进行反馈的居民中至少有![]() 人的年龄在
人的年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中
六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中![]() ,各踢了
,各踢了![]() 场,
场, ![]() 各踢了
各踢了![]() 场,
场, ![]() 踢了
踢了![]() 场,且
场,且![]() 队与
队与![]() 队未踢过,
队未踢过, ![]() 队与
队与![]() 队也未踢过,则在第一周的比赛中,
队也未踢过,则在第一周的比赛中, ![]() 队踢的比赛的场数是( )
队踢的比赛的场数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河南豫南九校高三下学期第一次联考】设函数![]() .
.
(I)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的范围;
的范围;
(II)若![]() 在
在![]() 处的切线为
处的切线为![]() ,且方程
,且方程![]() 恰有两解,求实数
恰有两解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站,且他们各自在每个站下车的可能性是相同的.
站,且他们各自在每个站下车的可能性是相同的.
(1)若甲、乙两人共付费![]() 元,则甲、乙下车方案共有多少种?
元,则甲、乙下车方案共有多少种?
(2)若甲、乙两人共付费![]() 元,求甲比乙先到达目的地的概率.
元,求甲比乙先到达目的地的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com