
【题目】已知函数![]() 是奇函数.
是奇函数.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)用定义证明函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
试题分析:(Ⅰ)由已知,函数![]() 是
是![]() 上的奇函数,则有
上的奇函数,则有![]() ,从而可解得
,从而可解得![]() ;(Ⅱ)用定义法证明函数单调性的步骤为:①取值,根据定义域(或指定的区域)任取
;(Ⅱ)用定义法证明函数单调性的步骤为:①取值,根据定义域(或指定的区域)任取![]() ,且
,且![]() ;②作差(或作商),
;②作差(或作商),![]() ,对其式子进行化简整理;③判断符号,即
,对其式子进行化简整理;③判断符号,即![]() ,或
,或![]() ;④下结论;(Ⅲ)由(Ⅰ)、(Ⅱ)可知函数
;④下结论;(Ⅲ)由(Ⅰ)、(Ⅱ)可知函数![]() 是奇函数,且在
是奇函数,且在![]() 上单调递增,则
上单调递增,则![]() ,等价于
,等价于![]() ,即
,即![]() ,再分离参数得
,再分离参数得![]() ,由不等式恒成立问题,从而可得解.
,由不等式恒成立问题,从而可得解.
试题解析:(Ⅰ)∵函数![]() 的定义域为R,且
的定义域为R,且![]() 是奇函数,∴
是奇函数,∴![]() ,解得
,解得![]()
此时![]() ,满足
,满足![]() ,即
,即![]() 是奇函数.
是奇函数.
∴![]() . …… 4分
. …… 4分
(Ⅱ) 任取![]() ,且
,且![]() ,则
,则![]() ,
,![]() ,
,
于是![]()
即![]() ,故函数
,故函数![]() 在
在![]() 上是增函数. …… 8分
上是增函数. …… 8分
(Ⅲ)由![]() 及
及![]() 是奇函数,知
是奇函数,知![]()
又由![]() 在
在![]() 上是增函数,得
上是增函数,得![]() ,即
,即![]() 对任意的
对任意的![]() 恒成立
恒成立
∵当![]() 时,
时,![]() 取最小值
取最小值![]() ,∴
,∴![]() …… 12分
…… 12分


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】下面是一个2×2列联表,则表中a、b的值分别为 ( )
y1 | y2 | 合计 | |
x1 | a | 21 | 73 |
x2 | 2 | 25 | 27 |
合计 | b | 46 | 100 |
A. 94、96 B. 52、50
C. 52、54 D. 54、52
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.
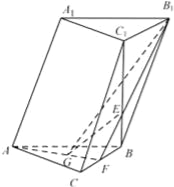
(1)求证:GE∥平面AA1B1B;
(2)平面AFB1分此棱柱为两部分,求这两部分体积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(1)若此方程表示圆,求![]() 的取值范围;
的取值范围;
(2)若(1)中的圆与直线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() ;
;
(3)在(2)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正整数排成下表:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
……………
则在表中数字2017出现在( )
A. 第44行第80列 B. 第45行第80列 C. 第44行第81列 D. 第45行第81列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com