
【题目】如图,已知一个八面体的各条棱长均为![]() ,四边形
,四边形![]() 为正方形,给出下列命题:
为正方形,给出下列命题:

①不平行的两条棱所在的直线所成的角是![]() 或
或![]() ; ②四边形
; ②四边形![]() 是正方形;
是正方形;
③点![]() 到平面
到平面![]() 的距离为
的距离为![]() ; ④平面
; ④平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.
其中正确的命题全部序号为_________________
【答案】①②③④
【解析】
利用八面体的结构特征逐条验证即可.
因为八面体的各条棱长均为1,四边形ABCD为正方形,
所以在四棱锥E﹣ABCD中,相邻两条侧棱所成的角为60°,而像AE与CE所成的角为90°,①正确
因为AE=CE=1,AC=![]() ,满足勾股定理的逆定理,所以AE⊥CE,同理AF⊥CF,AE⊥AF,所以四边形AECF是正方形;故②正确;
,满足勾股定理的逆定理,所以AE⊥CE,同理AF⊥CF,AE⊥AF,所以四边形AECF是正方形;故②正确;
设点A到平面BCE的距离h,由VE﹣ABCD=2VA﹣BCE,所以![]() ,解得h=
,解得h=![]() ;所以点A到平面BCE的距离
;所以点A到平面BCE的距离![]() ;故③正确;
;故③正确;
设平面![]() 与平面
与平面![]() 交线为m,显然m平行BC,
交线为m,显然m平行BC,
取AD的中点为P,BC的中点为Q,则PE⊥m,QE⊥m
故∠PEQ为平面![]() 与平面
与平面![]() 所成的锐二面角的平面角
所成的锐二面角的平面角
易知:PQ=1,PE=QE=![]() ,∴cos∠PEQ=
,∴cos∠PEQ= ,故④正确.
,故④正确.
故答案为:①②③④


科目:高中数学 来源: 题型:
【题目】对平面区域![]() ,用
,用![]() 表示属于
表示属于![]() 的所有整点(即
的所有整点(即![]() 平面上坐标
平面上坐标![]() 都是整数的点)的个数.若
都是整数的点)的个数.若![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界);
所围成的区域(包括边界);![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界).则
所围成的区域(包括边界).则![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在一次射击预选赛中,甲、乙两人各射击![]() 次,两人成绩的条形统计图如图所示,则下列四个选项中判断不正确的是( )
次,两人成绩的条形统计图如图所示,则下列四个选项中判断不正确的是( )

A. 甲的成绩的平均数小于乙的成绩的平均数
B. 甲的成绩的中位数小于乙的成绩的中位数
C. 甲的成绩的方差大于乙的成绩的方差
D. 甲的成绩的极差小于乙的成绩的极差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区1000位居民2018年12月份的用电情况进行统计后,按用电量分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
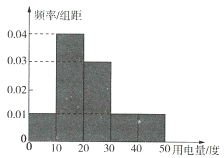
A.按用电量分组中,人数最多的一组有400人
B.12月份用电不低于20度的有500人
C.12月份人均用电量为25度
D.12月份的用电量的中位数是20度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:
支持 | 中立 | 不支持 | |
20岁以下 | 800 | 450 | 200 |
20岁及以上 | 100 | 150 | 300 |
在所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,已知从持“支持”态度的人抽取了45人,则
人,已知从持“支持”态度的人抽取了45人,则![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知第二小组的频数是40.

(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数;
(3)求这两个班参赛学生的成绩的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美,定义:能够将圆![]() 的周长和面积同时等分成两个部分的函数称为圆
的周长和面积同时等分成两个部分的函数称为圆![]() 的一个“太极函数”,则下列有关说法中:
的一个“太极函数”,则下列有关说法中:

①对于圆![]() 的所有非常数函数的太极函数中,一定不能为偶函数;
的所有非常数函数的太极函数中,一定不能为偶函数;
②函数![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
③存在圆![]() ,使得
,使得![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
④直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() 的太极函数;
的太极函数;
⑤若函数![]() 是圆
是圆![]() 的太极函数,则
的太极函数,则![]()
所有正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,各个侧面均是边长为
中,各个侧面均是边长为![]() 的正方形,
的正方形,![]() 为线段
为线段![]() 的中点.
的中点.
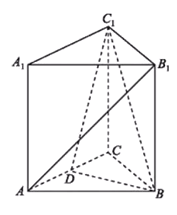
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)设![]() 为线段
为线段![]() 上任意一点,在
上任意一点,在![]() 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com