练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，E，F分别是棱AA1，AD上的点，且AE=EA1，AFFD.

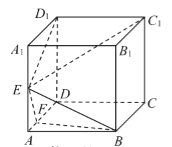
    （1）求证：平面EC1D1⊥平面EFB；

    （2）求二面角E﹣FB﹣A的余弦值.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）以为坐标原点，以为轴，为单位长，建立空间直角坐标系，利用向量法能证明平面平面．

    （2）求出平面的法向量和平面的法向量，利用向量法能求出二面角的余弦值．

    证明：（1）以为坐标原点，以为轴，为单位长，建立如图所示的空间直角坐标系，

    则，0，，，0，，，4，，，0，，，4，，

    ，4，，，0，，，0，，，4，，

    设平面的法向量，

    则，取，得，

    设平面的法向量，

    则，取，得，

    ，，

    平面平面．

    解：（2）由题意得平面的法向量可取，0，，

    由（1）知平面的法向量，，，

    设二面角的平面角为，

    则，

    二面角的余弦值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2018年国际乒联总决赛在韩国仁川举行，比赛时间为12月13﹣12月16日，在男子单打项目，中国队准备选派4人参加.已知国家一线队共6名队员，二线队共4名队员.

    （1）求恰好有3名国家一线队队员参加比赛的概率；

    （2）设随机变量X表示参加比赛的国家二线队队员的人数，求X的分布列；

    （3）男子单打决赛是林高远（中国）对阵张本智和（日本），比赛采用七局四胜制，已知在每局比赛中，林高远获胜的概率为，张本智和获胜的概率为，前两局比赛双方各胜一局，且各局比赛的结果相互独立，求林高远获得男子单打冠军的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在处取得极小值．

    （1）求实数的值；

    （2）设，讨论函数的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年1月18日，国家禁毒办召开视频会议，部署开展全国禁毒示范城市创建活动，会上，贵阳成功入选为首批全国101个示范创建城市之一.为进一步推进创建工作的开展，贵阳市教育局全面部署了各中小学深入学习禁毒知识的工作.某校据此开展相关禁毒知识测试活动，如图的茎叶图是该校从甲、乙两个班级各随机抽取5名同学在一次禁毒知识测试中的成绩统计

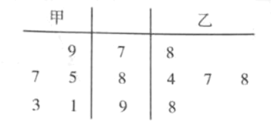
    （1）请从统计学角度分析两个班级的同学在禁毒知识学习上的状况；

    （2）由于测试难度较大，测试成绩达到87分以上（含87分）者即视为合格，先从茎叶图中达到合格的同学中抽取三人进行成绩分析，试求抽取到的同学中至少有两人来自甲班的概率；

    （3）已知本次测试的成绩服从正态分布，该校共有1000名同学参加了测试，求测试成绩在86分到97分之间的人数.

    （参考数据，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，多面体中，平面平面，，四边形为平行四边形.

    （1）证明：；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校在学期结束，为了解家长对学校工作的满意度，对两个班的100位家长进行满意度调查，调查结果如下：

    非常满意

    满意

    合计

    A

    30

    15

    45

    B

    45

    10

    55

    合计

    75

    25

    100

    （1）根据表格判断是否有的把握认为家长的满意程度与所在班级有关系？

    （2）用分层抽样的方法从非常满意的家长中抽取5人进行问卷调查，并在这5人中随机选出2人进行座谈，求这2人都来自同一班级的概率？

    附：

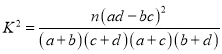
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，△DAB≌△DCB，E为线段BD上的点，且EA＝EB＝ED＝AB，延长CE交AD于点F．

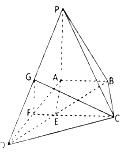
    （1）若G为PD的中点，求证平面PAD⊥平面CGF；

    （2）若AD＝AP＝6，求平面BCP与平面DCP所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，底面是直角梯形，，，且.点是线段上一点，且.

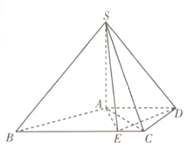
    （1）求证：平面平面.

    （2）若，在线段上是否存在一点，使得到平面的距离为？若存在，求的值；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案