
分析 根据二倍角公式和诱导公式,得到$\frac{\sqrt{3}}{2}$cosα+$\frac{\sqrt{2}}{2}$cosβ=0,①,sinα=$\sqrt{2}$sinβ,②,求出cos2α=$\frac{1}{2}$,cos2β=$\frac{3}{4}$,继而求出α=$\frac{π}{4}$,β=$\frac{π}{6}$,问题得以解决.
解答 解∵∵$\sqrt{3}$cos2$\frac{α}{2}$+$\sqrt{2}$sin2$\frac{β}{2}$=$\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{3}}}{2}$,
∴$\frac{\sqrt{3}}{2}$(1+cosα)+$\frac{\sqrt{2}}{2}$(1-cosβ)=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$,
∴$\frac{\sqrt{3}}{2}$cosα+$\frac{\sqrt{2}}{2}$cosβ=0,①
∵sin(2017π-α)=$\sqrt{2}$cos($\frac{5π}{2}$-β),
∴sinα=$\sqrt{2}$sinβ,②,
由①②,解得cos2α=$\frac{1}{2}$,cos2β=$\frac{3}{4}$,
∵α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),
∴α=$\frac{π}{4}$,β=$\frac{π}{6}$,
∴α+β=$\frac{5π}{12}$,
故答案为:$\frac{5π}{12}$
点评 本题考查了二倍角公式和诱导公式,以及同角的三角函数的关系和特殊角的三角函数值,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{8}{3}$ | B. | $\frac{8}{3}$ | C. | -$\frac{15}{8}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,16] | B. | [2,10] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {2} | C. | {-1,2} | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
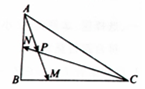 在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$
在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{\sqrt{2}}{2}$) | B. | (-∞,$\sqrt{2}$) | C. | (-∞,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,$\frac{9}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com