
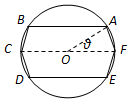
 某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.
某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.分析 (1)作AH⊥CF于H,则六边形的面积为f (θ)=2(cosθ+1)sinθ,θ∈(0,$\frac{π}{2}$).
(2)求导,分析函数的单调性,进而可得θ=$\frac{π}{3}$时,f (θ)取最大值.
解答 (本题满分16分)
解:(1)作AH⊥CF于H,
则OH=cosθ,AB=2OH=2cosθ,AH=sinθ,…(2分)
则六边形的面积为f (θ)=2×$\frac{1}{2}$(AB+CF)×AH=(2cosθ+2)sinθ
=2(cosθ+1)sinθ,θ∈(0,$\frac{π}{2}$). …(6分)
(2)f′(θ)=2[-sinθsinθ+(cosθ+1)cosθ]
=2(2cos2θ+cosθ-1)=2(2cosθ-1)(cosθ+1). …(10分)
令 f′(θ)=0,因为θ∈(0,$\frac{π}{2}$),
所以cosθ=$\frac{1}{2}$,即θ=$\frac{π}{3}$,…(12分)
当θ∈(0,$\frac{π}{3}$)时,f′(θ)>0,所以f (θ)在(0,$\frac{π}{3}$)上单调递增;
当θ∈($\frac{π}{3}$,$\frac{π}{2}$)时,f′(θ)<0,所以f (θ)在($\frac{π}{3}$,$\frac{π}{2}$)上单调递减,…(14分)
所以当θ=$\frac{π}{3}$时,f (θ)取最大值f ($\frac{π}{3}$)=2(cos$\frac{π}{3}$+1)sin$\frac{π}{3}$=$\frac{3\sqrt{3}}{2}$. …(15分)
答:当θ=$\frac{π}{3}$时,可使得六边形区域面积达到最大,最大面积为$\frac{3\sqrt{3}}{2}$平方百米.…(16分)
点评 本题考查的知识点是三角函数的实际应用,利用导数研究函数的最大值,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 22-n | B. | 2n-2 | C. | 2n+2 | D. | 2-n-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-2,2] | C. | (-2,2) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1] | B. | [-2,-1] | C. | (-∞,-2]∪[-1,+∞) | D. | (-∞,-2)∪(-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在六面体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1.
如图,在六面体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com