
����Ŀ����A�ǵ�λԲx2+y2=1�ϵ�����һ�㣬l�ǹ���A��x�ᴹֱ��ֱ�ߣ�D��ֱ��l��x��Ľ��㣬��M��ֱ��l�ϣ�������حDMح=mحDAح��m��0����m��1��������A��Բ���˶�ʱ���ǵ�M�Ĺ켣Ϊ����C��
��I��������C�ķ��̣��ж�����CΪ����Բ���ߣ��������ꣻ
����ԭ����б��Ϊk��ֱ�߽�����C��P��Q���㣬����P�ڵ�һ���ޣ�����y���ϵ���ӰΪ��N��ֱ��QN������C����һ��H���Ƿ����m��ʹ�ö������k��0������PQ��PH�������ڣ���m��ֵ���������ڣ���˵�����ɣ�
���𰸡��⣺��I����ͼ1����M��x��y����A��x0 �� y0��
��حDMح=mحDAح����x=x0 �� |y|=m|y0|
��x0=x��|y0|= ![]() |y|��
|y|��
�ߵ�A��Բ���˶����� ![]() ��
��
�ٴ���ڼ�����������C�ķ���Ϊ ![]()
��m�ʣ�0��1���ȣ�1��+�ޣ���
��0��m��1ʱ������C�ǽ�����x���ϵ���Բ������������ֱ�Ϊ�� ![]() ����
���� ![]()
m��1ʱ������C�ǽ�����y���ϵ���Բ������������ֱ�Ϊ�� ![]() ����
���� ![]()
������ͼ2��3��x1�ʣ�0��1������P��x1 �� y1����H��x2 �� y2������Q����x1 �� ��y1����N��0��y1����
��P��H��������ԲC�ϣ��� 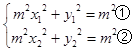
�٩��ڿɵ� ![]() ��
��
��Q��N��H���㹲�ߣ���kQN=kQH �� �� ![]()
��kPQkPH= ![]()
��PQ��PH����kPQkPH=��1
�� ![]()
��m��0���� ![]()
�ʴ��� ![]() ��ʹ�������Ӧ����Բ
��ʹ�������Ӧ����Բ ![]() �ϣ�������k��0������PQ��PH
�ϣ�������k��0������PQ��PH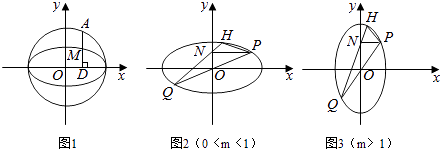
����������I����M��x��y����A��x0 �� y0��������حDMح=mحDAح��ȷ������֮��Ĺ�ϵx0=x��|y0|= ![]() |y|�����õ�A��Բ���˶�������������C�ķ��̣�����m�ʣ�0��1���ȣ�1��+�ޣ����������ۣ���ȷ���������ꣻ����x1�ʣ�0��1������P��x1 �� y1����H��x2 �� y2������Q����x1 �� ��y1����N��0��y1��������P��H��������ԲC�ϣ��ɵ�
|y|�����õ�A��Բ���˶�������������C�ķ��̣�����m�ʣ�0��1���ȣ�1��+�ޣ����������ۣ���ȷ���������ꣻ����x1�ʣ�0��1������P��x1 �� y1����H��x2 �� y2������Q����x1 �� ��y1����N��0��y1��������P��H��������ԲC�ϣ��ɵ� ![]() ���Ӷ��ɵÿɵ�
���Ӷ��ɵÿɵ� ![]() ������Q��N��H���㹲�ߣ���PQ��PH��������ý��ۣ�
������Q��N��H���㹲�ߣ���PQ��PH��������ý��ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x|x|��mx+1��������㣬��ʵ��m��ȡֵ��Χ�ǣ� ��
A.��0��2��
B.��2��+�ޣ�
C.�����ޣ���2��
D.[2��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��ֱ��
��ֱ��![]() ��E����A��B���㣬��
��E����A��B���㣬��![]() ������OΪԭ��.
������OΪԭ��.
��1����������E�ķ��̣�
��2����C����Ϊ![]() ����ֱ��CA��CB��б�ʷֱ�Ϊ
����ֱ��CA��CB��б�ʷֱ�Ϊ![]() ��֤����
��֤���� ![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������{an}��ǰn���ΪSn����a1��1��![]() ��Sn��1��Sn.
��Sn��1��Sn.
(1)��{an}��ͨ�ʽ��
(2)��![]() ��������{bn}��ǰn���Tn.
��������{bn}��ǰn���Tn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ǡ�ABC�У�a��b��c�ֱ�Ϊ�ڽ�A��B��C���Աߵı߳���������![]() a��2bsin A��0.
a��2bsin A��0.
(1)���B�Ĵ�С��
(2)��a��c��5����a>c��b��![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڳ�����ABCD-A1B1C1D1��,AB=BC=1,AA1=2,E�Dz���BB1���е�,��ֱ��AE��ƽ��A1ED1���ɽǵĴ�СΪ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ABCD�DZ߳�Ϊ3��������,DE��ƽ��ABCD,AF��DE,DE=3AF,BE��ƽ��ABCD���ɽ�Ϊ60��.
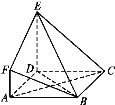
(1)������F-BE-D������ֵ;
(2)���M���߶�BD��һ������,��ȷ����M��λ��,ʹ��AM��ƽ��BEF,��֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x��1|+|x��2|
��1����ʽf��x����3�Ľ⼯��
��2��������ʽ||a+b|��|a��b||��|a|f��x����a��0��a��R��b��R�����������ʵ��x�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵�����ٽ�һ�������е�ÿ�����ݶ����ϻ��ȥͬһ����������㲻�䣻������һ���ع鷽��![]() ��3��5x������x����һ����λʱ��yƽ������5����λ�������Իع鷽��
��3��5x������x����һ����λʱ��yƽ������5����λ�������Իع鷽��![]() ��
��![]() x���ع�(
x���ع�(![]() ��
��![]() )���������ϵĵ���õ������֮�������ع�ϵ������һ��2��2�������У��ɼ����K2��13.079��������������֮���й�ϵ�Ŀ�������90%.���д���ĸ�����________��
)���������ϵĵ���õ������֮�������ع�ϵ������һ��2��2�������У��ɼ����K2��13.079��������������֮���й�ϵ�Ŀ�������90%.���д���ĸ�����________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com