
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】定义域是![]() 上的连续函数
上的连续函数![]() 图像的两个端点为
图像的两个端点为![]() 、
、![]() ,
,![]() 是图像
是图像![]() 上任意一点,过点
上任意一点,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交线段
交线段![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 可以重合),我们称
可以重合),我们称![]() 的最大值为该函数的“曲径”,下列定义域是
的最大值为该函数的“曲径”,下列定义域是![]() 上的函数中,曲径最小的是( )
上的函数中,曲径最小的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
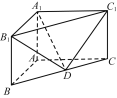
【题目】在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点.
(1) 求直线DC1与平面A1B1D所成角的正弦值;
(2) 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地实行垃圾分类后,政府决定为![]() 三个小区建造一座垃圾处理站M,集中处理三个小区的湿垃圾.已知
三个小区建造一座垃圾处理站M,集中处理三个小区的湿垃圾.已知![]() 在
在![]() 的正西方向,
的正西方向,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,
方向,![]() 在
在![]() 的北偏西
的北偏西![]() 方向,且在
方向,且在![]() 的北偏西
的北偏西![]() 方向,小区
方向,小区![]() 与
与![]() 相距
相距![]() 与
与![]() 相距
相距![]() .
.
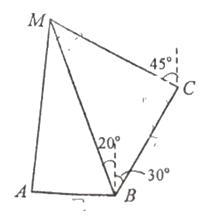
(1)求垃圾处理站![]() 与小区
与小区![]() 之间的距离;
之间的距离;
(2)假设有大、小两种运输车,车在往返各小区、处理站之间都是直线行驶,一辆大车的行车费用为每公里![]() 元,一辆小车的行车费用为每公里
元,一辆小车的行车费用为每公里![]() 元(其中
元(其中![]() 为满足
为满足![]() 是
是![]() 内的正整数) .现有两种运输湿垃圾的方案:
内的正整数) .现有两种运输湿垃圾的方案:
方案1:只用一辆大车运输,从![]() 出发,依次经
出发,依次经![]() 再由
再由![]() 返回到
返回到![]() ;
;
方案2:先用两辆小车分别从![]() 运送到
运送到![]() ,然后并各自返回到
,然后并各自返回到![]() ,一辆大车从
,一辆大车从![]() 直接到
直接到![]() 再返回到
再返回到![]() .试比较哪种方案更合算?请说明理由. 结果精确到小数点后两位
.试比较哪种方案更合算?请说明理由. 结果精确到小数点后两位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着![]() 网络的普及和智能手机的更新换代,各种方便的
网络的普及和智能手机的更新换代,各种方便的![]() 相继出世,其功能也是五花八门.某大学为了调查在校大学生使用
相继出世,其功能也是五花八门.某大学为了调查在校大学生使用![]() 的主要用途,随机抽取了
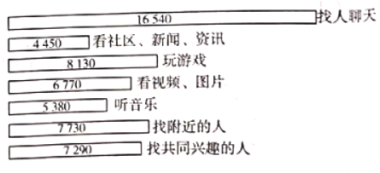
的主要用途,随机抽取了![]() 名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
①可以估计使用![]() 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
②可以估计不足![]() 的大学生使用
的大学生使用![]() 主要玩游戏;
主要玩游戏;
③可以估计使用![]() 主要找人聊天的大学生超过总数的
主要找人聊天的大学生超过总数的![]() .
.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )

A.33B.56C.64D.78
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何是美籍法国数学家芒德勃罗在20世纪70年代创立的一门数学新分支,其中的“谢尔宾斯基”图形的作法是:先作一个正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的每个小正三角形中又挖去一个“中心三角形”.按上述方法无限连续地作下去直到无穷,最终所得的极限图形称为“谢尔宾斯基”图形(如图所示),按上述操作7次后,“谢尔宾斯基”图形中的小正三角形的个数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数据![]() 是郑州市普通职工
是郑州市普通职工![]() 个人的年收入,若这
个人的年收入,若这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于一个项数为![]() 的数列
的数列![]() ,若存在
,若存在![]() 且
且![]() ,使得数列
,使得数列![]() 的前k项和与剩下项的和相等(若仅为1项,则和为该项本身),我们称该数列是“等和数列”.例如:因为
的前k项和与剩下项的和相等(若仅为1项,则和为该项本身),我们称该数列是“等和数列”.例如:因为![]() ,所以数列3,2,1是“等和数列”.请解答以下问题:
,所以数列3,2,1是“等和数列”.请解答以下问题:
(1)数列1,2,p,4是“等和数列”,求实数p的值;
(2)项数为![]() 的等差数列
的等差数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,求证:
,求证:![]() 是“等和数列”.
是“等和数列”.
(3)![]() 是公比为q项数为
是公比为q项数为![]() 的等比数列
的等比数列![]() ,其中
,其中![]() 且
且![]() 恒成立.判断
恒成立.判断![]() 是不是“等和数列”,并证明你的结论.
是不是“等和数列”,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com