
分析 (1)由$(\overrightarrow{a}+2\overrightarrow{b})•(2\overrightarrow{a}-\overrightarrow{b})$=2${\overrightarrow{a}}^{2}$+3$\overrightarrow{a}•\overrightarrow{b}$-2${\overrightarrow{b}}^{2}$=-20,能求出$\overrightarrow{\;a\;}$与$\overrightarrow{\;b\;}$的夹角.
(2)由$(k\overrightarrow{a}+\overrightarrow{b})(\overrightarrow{a}-\overrightarrow{b})$=$k{\overrightarrow{a}}^{2}+(1-k)\overrightarrow{a}•\overrightarrow{b}-{\overrightarrow{b}}^{2}$=0,能求出k.
解答 解:(1)∵$|{\overrightarrow{\;a\;}}|=3$,$|{\overrightarrow{\;b\;}}|=4$,$({\overrightarrow{\;a\;}+2\overrightarrow{\;b\;}})•({2\overrightarrow{\;a\;}-\overrightarrow{\;b\;}})=-20$,
∴$(\overrightarrow{a}+2\overrightarrow{b})•(2\overrightarrow{a}-\overrightarrow{b})$=2${\overrightarrow{a}}^{2}$+3$\overrightarrow{a}•\overrightarrow{b}$-2${\overrightarrow{b}}^{2}$
=2×9-2×16+3×3×4×cos<$\overrightarrow{a},\overrightarrow{b}$>=-20,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=-$\frac{1}{6}$,
∴<$\overrightarrow{a},\overrightarrow{b}$>=arccos(-$\frac{1}{6}$)=$π-arccos\frac{1}{6}$.
∴$\overrightarrow{\;a\;}$与$\overrightarrow{\;b\;}$的夹角为$π-arccos\frac{1}{6}$.
(2)∵$|{\overrightarrow{\;a\;}}|=3$,$|{\overrightarrow{\;b\;}}|=4$,$\overrightarrow{\;a\;}$与$\overrightarrow{\;b\;}$的夹角为60°,$k\overrightarrow{\;a\;}+\overrightarrow{\;b\;}$与$\overrightarrow{\;a\;}-\overrightarrow{\;b\;}$垂直,
∴$(k\overrightarrow{a}+\overrightarrow{b})(\overrightarrow{a}-\overrightarrow{b})$=$k{\overrightarrow{a}}^{2}+(1-k)\overrightarrow{a}•\overrightarrow{b}-{\overrightarrow{b}}^{2}$=0,
∴9k+(1-k)×3×4×cos60°-16=0,
解得k=$\frac{10}{3}$.
点评 本题考查向量的夹角的求法,考查实数值的求法,是基础题,解题时要认真审题,注意向量数量积公式的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
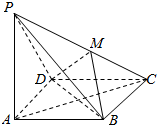 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{6\sqrt{2}}{13}$ | D. | $\frac{5\sqrt{2}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com