
| 平面几何选讲 | 极坐标与参数方程 | 不等式选讲 | 合计 | |
| 男同学(人数) | 12 | 4 | 6 | 22 |
| 女同学(人数) | 8 | 12 | 20 | |
| 合计 | 12 | 12 | 18 | 42 |
| 几何类 | 代数类 | 合计 | |
| 男同学(人数) | 16 | 6 | 22 |
| 女同学(人数) | 8 | 12 | 20 |
| 合计 | 24 | 18 | 42 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
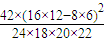 =
=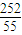 ≈4.582>3.841.
≈4.582>3.841.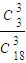 ,P(A)=
,P(A)= .
.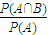 =
=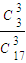 =
=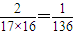 .…(8分)
.…(8分)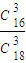 =
=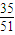 ;P(X=1)=
;P(X=1)=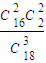 =
=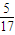 ;
;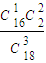 =
=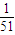 .…(10分)
.…(10分)| X | 1 | 2 | |
| P | 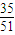 | 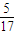 | 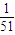 |
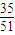 +1×
+1×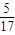 +2×
+2×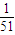 =
= .…(12分)
.…(12分)

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
 6、某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有( )人.
6、某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有( )人.查看答案和解析>>
科目:高中数学 来源:黑龙江省庆安一中2009-2010学年高二上学期期中考试数学试题 题型:044
在一次数学测验后,数学老师将某班全体学生(50人)的数学成绩进行初步统计后交给班主任(如下表)
请你帮助这位班主任完成下面的统计分析工作:
(1)列出频率分布表;
(2)画出频率分布直方图及频率分布折线图;
(3)从频率分布直方图中估计出该班同学数学成绩的众数、平均数.
(1)样本频率分布表如下:

(2)频率分布直方图和折线图如下:
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
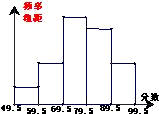 某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有人.
某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有人.查看答案和解析>>
科目:高中数学 来源:2009-2010学年河南省洛阳市高一(上)期中数学试卷(必修1)(解析版) 题型:选择题
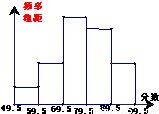
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com