
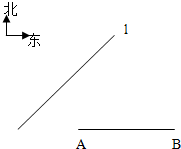
 如图,某开发区旁边有一条东北走向的公路l,开发区内有两工厂A,B(B在A正东4km),A工厂到公路l的距离为(
如图,某开发区旁边有一条东北走向的公路l,开发区内有两工厂A,B(B在A正东4km),A工厂到公路l的距离为(| 6 |
| 2 |
| 2 |
| 6 |
| 2 |
| x2 |
| b2+4 |
| y2 |
| b2 |
|
| x2 |
| 8 |
| y2 |
| 4 |
| x2 |
| 8 |
| y2 |
| 4 |
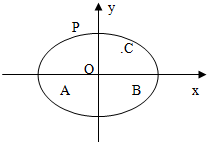 解:以A,B所在直线为x轴,中点为原点,建立直角坐标系,则A(-2,0),B(2,0),
解:以A,B所在直线为x轴,中点为原点,建立直角坐标系,则A(-2,0),B(2,0),| |-2+m| | ||
|
| 6 |
| 2 |
| 3 |
| 3 |
| 3 |
| x2 |
| b2+4 |
| y2 |
| b2 |
|
| 3 |
| 3 |
| x2 |
| 8 |
| y2 |
| 4 |
| x2 |
| 8 |
| y2 |
| 4 |
| x2 |
| 8 |
| y2 |
| 4 |
|
|
|
-4+12
| ||
| 11 |
6+4
| ||
| 11 |
| 10 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2005-2006学年江苏省南通市高二(上)期末数学试卷(解析版) 题型:解答题
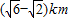 .建立适当的坐标系,解决下列问题:
.建立适当的坐标系,解决下列问题: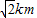 ,在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小.试问:满足要求的点N在什么位置(不要证明),并求|NC|+|NB|的值.
,在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小.试问:满足要求的点N在什么位置(不要证明),并求|NC|+|NB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com