
����Ŀ��ij��ѧ�����Ŀư�ѧ���μ�����ѧ�����ˮƽ���ԣ�ѧУ�Ӳ��Ժϸ��ѧ���������ȡ100�˵ijɼ�����ͳ�Ʒ���.��ȡ��100�˵���ѧ�������ˮƽ���Գɼ����±���

�ɼ���Ϊ���㡢���á����������ȼ�����������ֱ��ʾ�����ɼ�����ѧ�ɼ������磺������ѧ�ɼ�Ϊ���õĹ���20+18+4=42��.
��1�����ڸ������У���ѧ�ɼ�������Ϊ30%����a��b��ֵ��
��2����������![]() �����ڵ����ɼ������ѧ���У���ѧ�ɼ�����������ȼ���������ٵĸ���.
�����ڵ����ɼ������ѧ���У���ѧ�ɼ�����������ȼ���������ٵĸ���.
���𰸡���1��![]() ��
�� ![]() �� ��2��
�� ��2��![]() .
.
�������������������1����![]() ����
����![]() =14���ɴ������b��ֵ����2�������⣬֪a+b=31����a��10��b��8�����оٷ���������������ģ�a��b����14�飬��ÿ����ֵĿ�������ͬ���ҳ�������ѧ�ɼ�����������ȼ���������ٵ���6�飬���ݸ��ʹ�ʽ���㼴�ɣ�
=14���ɴ������b��ֵ����2�������⣬֪a+b=31����a��10��b��8�����оٷ���������������ģ�a��b����14�飬��ÿ����ֵĿ�������ͬ���ҳ�������ѧ�ɼ�����������ȼ���������ٵ���6�飬���ݸ��ʹ�ʽ���㼴�ɣ�
���������
��1����![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
�� ![]() ��
��
��2��������֪![]() ����
����![]() ��
��
������������![]() ��
��![]() ,
,
![]() ��14��.
��14��.
��ÿ����ֵĿ�������ͬ.
������ѧ�ɼ�����������ȼ���������ٵ��У�
![]() ��6��.
��6��.
����ѧ�ɼ�Ϊ����������ȼ���������ٵĸ���Ϊ![]() .
.


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�Ķ������У�����ABCDΪ�����Σ���GADΪ�ȱ������Σ�BF��ƽ��ABCD����GDC��90�㣬��E���߶�GC�ϳ����˵����һ�㣬����PΪ�߶�GD���е㣮
(��)��֤��AP��ƽ��GCD��
(��)��֤��ƽ��ADG��ƽ��FBC��
(��)��AP��ƽ��BDE����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�CC1��ƽ��ABC��M��CC1�е㣮

(��)��֤��ƽ��AB1M��ƽ��A1ABB1��
(��)����C��һ������ƽ��AB1Mƽ�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() (a>b>0)�����᳤Ϊ4��������Ϊ
(a>b>0)�����᳤Ϊ4��������Ϊ![]() .
.
(��)��Բ������Բ�ı����̣�
(��)�������M(0,2)��ֱ��l����ԲC���ڲ�ͬ������A��B���ҡ�AOBΪ���(OΪ����ԭ��)����ֱ��l��б��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У� ![]() ��
�� ![]() ��
��
(1)��![]() ����f(A)��0�����A��ֵ��
����f(A)��0�����A��ֵ��
(2)���������ʵ��t������![]() �����ABC��������ֵ��
�����ABC��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��ѧ�ţ�05856261)
ij��ҵԱ��500�˲μӡ�ѧ�桱־Ը�����������飺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ����5��
����5��![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
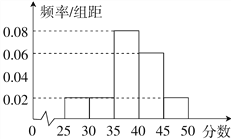
(��)�±��������Ƶ�ʷֲ�������������a��b��ֵ��

(��)����Ҫ�������С�ĵ�1,2,3�����÷ֲ�����ķ�����ȡ6�ˣ������ڵ�1,2,3���ȡ��Ա���������ֱ��Ƕ��٣�
(��)��(��)��ǰ���£�����6���������ȡ2�˲μ������������������������1�������ڵ�3��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
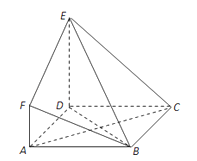
����Ŀ����ͼ��ABCD�DZ߳�Ϊ3�������Σ�DE��ƽ��ABCD��AF��DE��DE=3AF��BE��ƽ��ABCD���ɽ�Ϊ60����
��������֤��AC��ƽ��BDE��
������������F��BE��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��2000����һ��������Ӣ���س�����ѡ�Σ��ֳ�ȡ����ѧ����Ӣ��ɼ�������������������ó�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��ͼ�д����Ҹ�С���������֮��Ϊ![]() ���ڶ�С��Ƶ��Ϊ12��
���ڶ�С��Ƶ��Ϊ12��

��������ڶ�С���Ƶ�ʼ���ȡ��ѧ��������
��������������120����������120���������ʸ�¼ȡ��Լ�ж���ѧ�����ʸ�¼ȡ��
������ѧУ����ӷ�����![]() ��
��![]() ���ڵ�ѧ���У����ֲ������ȡ4�˽��иĽ�����ʾ����飬��������ʦ�������4�˵��ʾ�����ÿ��һ���������ȡ���ݵ��ģ����������ʾ�������Ӣ����Գɼ���
���ڵ�ѧ���У����ֲ������ȡ4�˽��иĽ�����ʾ����飬��������ʦ�������4�˵��ʾ�����ÿ��һ���������ȡ���ݵ��ģ����������ʾ�������Ӣ����Գɼ���![]() �ֵ�ѧ���ĸ��ʣ�
�ֵ�ѧ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
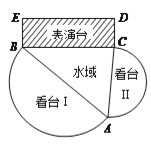
����Ŀ����һˮ���Ͻ�һ�����չ㳡.���չ㳡�ɿ�̨��̨��������ˮ��![]() �������α���̨
�������α���̨![]() �ĸ����ֹ��ɣ���ͼ��.��̨��̨���Ƿֱ���
�ĸ����ֹ��ɣ���ͼ��.��̨��̨���Ƿֱ���![]() ��
�� ![]() Ϊֱ����������Բ�������ҿ�̨�������ǿ�̨��������3�������α���̨
Ϊֱ����������Բ�������ҿ�̨�������ǿ�̨��������3�������α���̨![]() �У�
�У� ![]() �ף�������ˮ��
�ף�������ˮ��![]() �����Ϊ
�����Ϊ![]() ƽ����.��
ƽ����.��![]() .
.
����![]() ʱ����
ʱ����![]() �ij���
�ij���
����������̨ÿƽ�������Ϊ![]() ��Ԫ�������̨��������.
��Ԫ�������̨��������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com