解:由题意得:sin(B+A)+sin(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,
当cosA=0时,则A=

,B=

,则a=2b,c=

b,又c+b=2+

,
所以b=

,c=
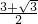
,所以S
△ABC=

bcsinA=
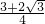
;
当cosA≠0时,得sinB=2sinA,由正弦定理得:b=2a,①
又由余弦定理得:cos

=
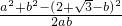
=

,②
将①代入②,解得a=1或a=7+4

>b+c=2+

(舍去),b=2,
此时c=

,所以△ABC是直角三角形,所以S
△ABC=

ac=

,
综上,△ABC的面积为
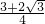
或

.
分析:根据三角形的内角和定理及诱导公式化简sinC+sin(B-A)=2sin2A,分cosA等于0和不等于0两种情况考虑,当cosA等于0时,得到A和B的度数,根据直角三角形中30°角所对的直角边等于斜边的一半,得到a=2b,c=

b,又c+b=2+

,即可求出b和c的值,根据三角形的面积公式即可求出△ABC的面积;当cosA不等于0时,得到sinB=2sinA,根据正弦定理得到b与a的关系式,记作①,再根据余弦定理表示出cos

的关系式,记作②,将①代入②即可求出a与b的值,进而得到c的值,根据勾股定理的逆定理判断得到△ABC是直角三角形,根据两直角边乘积的一半即可求出△ABC的面积,综上,得到△ABC的面积的两个值.
点评:此题考查学生灵活运用两角和与差的正弦函数公式及三角形的面积公式化简求值,灵活运用正弦、余弦定理化简求值,是一道中档题.

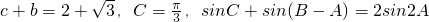 ,求△ABC的面积.
,求△ABC的面积. ,B=
,B= ,则a=2b,c=
,则a=2b,c= b,又c+b=2+
b,又c+b=2+ ,
, ,c=
,c=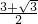 ,所以S△ABC=
,所以S△ABC= bcsinA=
bcsinA=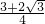 ;
; =
=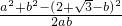 =
= ,②
,② >b+c=2+
>b+c=2+ (舍去),b=2,
(舍去),b=2, ,所以△ABC是直角三角形,所以S△ABC=
,所以△ABC是直角三角形,所以S△ABC= ac=
ac= ,
,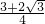 或
或 .
. b,又c+b=2+
b,又c+b=2+ ,即可求出b和c的值,根据三角形的面积公式即可求出△ABC的面积;当cosA不等于0时,得到sinB=2sinA,根据正弦定理得到b与a的关系式,记作①,再根据余弦定理表示出cos
,即可求出b和c的值,根据三角形的面积公式即可求出△ABC的面积;当cosA不等于0时,得到sinB=2sinA,根据正弦定理得到b与a的关系式,记作①,再根据余弦定理表示出cos 的关系式,记作②,将①代入②即可求出a与b的值,进而得到c的值,根据勾股定理的逆定理判断得到△ABC是直角三角形,根据两直角边乘积的一半即可求出△ABC的面积,综上,得到△ABC的面积的两个值.
的关系式,记作②,将①代入②即可求出a与b的值,进而得到c的值,根据勾股定理的逆定理判断得到△ABC是直角三角形,根据两直角边乘积的一半即可求出△ABC的面积,综上,得到△ABC的面积的两个值.

 字词句段篇系列答案
字词句段篇系列答案