
【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取![]() 人看成一个总体,从这
人看成一个总体,从这![]() 人中任意选取
人中任意选取![]() 人,求至少有一人年龄在
人,求至少有一人年龄在![]() 岁以下的概率.
岁以下的概率.
(3)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 概率.
概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由![]() 比上总人数等于30人比上持“不支持”态度的人数即可得解;
比上总人数等于30人比上持“不支持”态度的人数即可得解;
(2)列树状图,用古典概型计算即可;
(3)先计算平均数,再列举出与总体平均数之差的绝对值超过![]() 事件按,作比即可得解.
事件按,作比即可得解.
试题解析:
(1)参与调查的总人数为![]() ,其中从持“不支持”态度的人数
,其中从持“不支持”态度的人数![]() 中抽取了
中抽取了![]() 人,所以
人,所以![]() .
.
(2)易得,抽取的![]() 人中,
人中, ![]() 岁以下与
岁以下与![]() 岁以上人数分别为
岁以上人数分别为![]() 人(记为
人(记为![]() ,
, ![]() ),
),![]() 人(记为
人(记为![]() ,
, ![]() ,
, ![]() ),从这
),从这![]() 人中任意选取
人中任意选取![]() 人,基本事件为:
人,基本事件为:
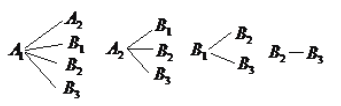
其中,至少有![]() 人年龄在
人年龄在![]() 岁以下的事件有
岁以下的事件有![]() 个,所求概率为
个,所求概率为![]() .
.
(3)总体的平均数为![]()
![]() ,
,
那么与总体平均数之差的绝对值超过![]() 的数有
的数有![]() ,
, ![]() ,
, ![]() ,所以任取
,所以任取![]() 个数与总体平均数之差的绝对值超过
个数与总体平均数之差的绝对值超过![]() 的概率为
的概率为![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 部分图象如图所示.
部分图象如图所示.
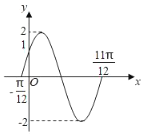
(1)求函数![]() 的解析式及
的解析式及![]() 的单调递增区间;
的单调递增区间;
(2)把函数![]() 图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移
图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于x的方程
的图象,求关于x的方程![]() 在
在![]() 上所有的实数根之和.
上所有的实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(cosωx-sinωx,sinωx),b=(-cosωx-sinωx,2![]() cosωx).设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈
cosωx).设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈![]() .
.
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点![]() ,求函数f(x)在区间
,求函数f(x)在区间![]() 上的取值范围
上的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量X(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量y(百斤)与使用某种液体肥料x(千克)之间对应数据为如图所示的折线图.

(1) 依据数据的折线图,是否可用线性回归模型拟合y与x的关系?请计算相关系数r并加以说明(精确到0.01)(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2) 蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量X限制,并有如表关系:
周光照量 |
|
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以过去50周的周光照量的频率作为周光照量发生的概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数 ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产一种机器的固定成本为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元,市场对此产品的年求量为500台,销售的收入函数为![]() (万元)(
(万元)(![]() ),其中
),其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com