
【题目】已知函数f(x)= ![]() +acosx,g(x)是f(x)的导函数.
+acosx,g(x)是f(x)的导函数.
(1)若f(x)在 ![]() 处的切线方程为y=
处的切线方程为y= ![]() ,求a的值;
,求a的值;
(2)若a≥0且f(x)在x=0时取得最小值,求a的取值范围;
(3)在(1)的条件下,当x>0时, ![]() .
.
【答案】
(1)解:f′(x)=x﹣asinx,
f′( ![]() )=
)= ![]() ﹣a=
﹣a= ![]() ,
,
∴a=﹣1,经验证a=﹣1合题意
(2)解:g(x)=f′(x)=x﹣asinx g′(x)=1﹣acosx
①当a=0时,f(x)= ![]() x2,显然在x=0时取得最小值,
x2,显然在x=0时取得最小值,
∴a=0合题意;
②当a>0时,
(i)当 ![]() ≥1即0<a≤1时,g′(x)≥0恒成立,
≥1即0<a≤1时,g′(x)≥0恒成立,
∴g(x)在(﹣∞,+∞)上单调递增,又g(0)=0
∴当x<0时,g(x)<0 即f′(x)<0,当x>0时,g(x)>0 即f′(x)>0
∴f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增;
∴f(x) 在x=0时取得最小值
∴当0<a≤1时合题意;
(ii)当0< ![]() <1即a>1时,在(0,π)内存在唯一x0=arccos
<1即a>1时,在(0,π)内存在唯一x0=arccos ![]() 使g′(x)=0
使g′(x)=0
当x∈(0,x0)时,
∵y=cosx在(0,π)上是单调递减的,
∴cosx>cosx0= ![]()
∴g′(x)=a ( ![]() ﹣cosx)<0,
﹣cosx)<0,
∴g(x) 在(0,x0)上单调递减,
∴g(x)<g(0)=0
即f′(x)<0,
∴f(x)在(0,x0)内单调递减;
∴x∈(0,x0)时,f(x)<0 这与f(x)在x=0时取得最小值即f(x)≥f(0)矛盾,
∴当a>1时不合题意;
综上,a的取值范围是0,1]
(3)解:由(1)知,a=﹣1 此时g(x)=x+sinx,g′(x)=1+cosx,
∴ ![]() =
= ![]() =|cos
=|cos ![]() |≥cos
|≥cos ![]() ,
,
∴若要证原不等式成立,只需证cos ![]() +
+ ![]() x2>
x2> ![]() 成立;
成立;
由(2)知,当a=1时,f(x)≥f(0)恒成立,即 ![]() x2+cosx≥1恒成立
x2+cosx≥1恒成立
即cosx≥1﹣ ![]() x2(当且仅当x=0时取“=“号),
x2(当且仅当x=0时取“=“号),
∴cos ![]() ≥1﹣
≥1﹣ ![]() x2(当且仅当x=0时取“=“号) …①
x2(当且仅当x=0时取“=“号) …①
∴只需证:1﹣ ![]() x2+
x2+ ![]() x2>
x2> ![]() 成立,即1+
成立,即1+ ![]() x2>
x2> ![]() ,
,
又由均值不等式知:1+ ![]() x2≥x(当且仅当x=2时取“=“号) …②
x2≥x(当且仅当x=2时取“=“号) …②
∵①②两个不等式取“=“的条件不一致,
∴只需证:x≥ ![]() ,
,
两边取对数得:lnx≥1﹣ ![]() …③
…③
下面证③式成立:令(x)=lnx﹣1+ ![]() ,
,
则′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴(x)在(0,1)上单调递减,在(1,+∞)上单调递增
∴(x)≥(1)=0,
即lnx﹣1+ ![]() ≥0,
≥0,
∴lnx≥1﹣ ![]() ,
,
即③式成立,
∴原不等式成立.
【解析】(1)先求导,根据导数和几何意义即可求出,(2)先求导,再分类讨论,根据导数和函数的最值得关系即可求出参数的取值范围,(3)原不等式转化为cos ![]() +
+ ![]() x2>
x2> ![]() 成立,分别根据均值不等式和导数和函数的最值得关系即可证明.
成立,分别根据均值不等式和导数和函数的最值得关系即可证明.
【考点精析】根据题目的已知条件,利用基本求导法则和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC中,AC=1, ![]() ,设∠BAC=x,记
,设∠BAC=x,记 ![]() ;
;
(1)求函数f(x)的解析式及定义域;
(2)试写出函数f(x)的单调递增区间,并求方程 ![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足不等式组  ,若目标函数z=kx+y仅在点(1,1)处取得最小值,则实数k的取值范围是 ( )
,若目标函数z=kx+y仅在点(1,1)处取得最小值,则实数k的取值范围是 ( )
A.(﹣1,+∞)
B.(﹣∞,﹣1)
C.(1,+∞)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上.
=1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上. 
(1)求椭圆C的方程;
(2)设点M(2,0),过点F1的直线交C于A,B两点,直线MA,MB与直线x=﹣2分别交于P,Q两点,求△MPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R且a<b,若a3eb=b3ea , 则下列结论中一定正确的个数是( ) ①a+b>6;②ab<9;③a+2b>9;④a<3<b.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)满足:函数y=f(x+1)的图象关于直线x=﹣1对称,且当x∈(﹣∞,0)时,f(x)+xf′(x)<0成立(f′(x)是函数f(x)的导函数),若a=0.76f(0.76),b=log ![]() 6f(log
6f(log ![]() 6),c=60.6f(60.6),则a,b,c的大小关系是( )
6),c=60.6f(60.6),则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.c>a>b
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a、b∈M,
(1)证明:| ![]() a+
a+ ![]() b|<
b|< ![]() ;
;
(2)比较|1﹣4ab|与2|a﹣b|的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六面体ABCD﹣A1B1C1D1中,M,N分别是棱A1B1 , B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1 . 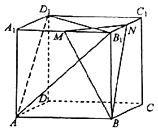
(1)证明:BB1⊥平面ABCD;
(2)已知六面体ABCD﹣A1B1C1D1的棱长均为 ![]() ,cos∠BAD=
,cos∠BAD= ![]() ,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五棱锥P﹣ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
(Ⅰ)求证:平面PBE⊥平面APG;
(Ⅱ)已知AB=2,BC= ![]() ,侧棱PA与底面ABCDE所成角为45°,S△PBE=
,侧棱PA与底面ABCDE所成角为45°,S△PBE= ![]() ,点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.
,点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com