
【题目】作为加班拍档、创业伴侣、春运神器,曾几何时,方便面是我们生活中重要的“朋友”,然而这种景象却在近![]() 年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续
年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续![]() 年保持两位数增长,2013年的年销量更是创下
年保持两位数增长,2013年的年销量更是创下![]() 亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩
亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩![]() 亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
全国方便面销量情况(单位“亿包/桶)(数据来源:世界方便面协会)
年份 |
|
|
|
|
时间代号 |
|
|
|
|
年销量 |
|
|
|
|
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2017 年(
.用所求回归方程预测2017 年(![]() )方便面在中国的年销量;
)方便面在中国的年销量;
(2)方便面销量遭遇滑铁卢受到哪些因素影响? 中国的消费业态发生了怎样的转变? 某媒体记者随机对身边的![]() 位朋友做了一次调查,其中
位朋友做了一次调查,其中![]() 位受访者表示超过
位受访者表示超过![]() 年未吃过方便面,
年未吃过方便面,![]() 位受访者认为方便面是健康食品;而
位受访者认为方便面是健康食品;而![]() 位受访者有过网络订餐的经历,现从这
位受访者有过网络订餐的经历,现从这![]() 人中抽取
人中抽取![]() 人进行深度访谈,记
人进行深度访谈,记![]() 表示随机抽取的
表示随机抽取的![]() 人认为方便面是健康食品的人数,求随机变量
人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中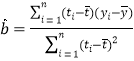 ,
,![]() .
.
参考数据:![]() .
.
科目:高中数学 来源: 题型:
【题目】“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
爱好 | 10 | ||
不爱好 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为![]() ,求
,求![]() 的分布列、数学期望.参考数据:
的分布列、数学期望.参考数据:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024/span> | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某校某次数学考试的情况,现从该校参加考试的600名学生中随机抽出60名学生,其数学成绩(百分制)均在![]() 内,将这些成绩分成六组
内,将这些成绩分成六组![]() …
…![]() ,得到如图所示的部分频率分布直方图.
,得到如图所示的部分频率分布直方图.
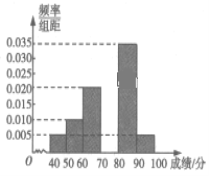
(1)求抽出的60名学生中数学成绩在![]() 内的人数;
内的人数;
(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校参加考试的学生数学成绩为优秀的人数;
(3)试估计抽出的60名学生的数学成绩的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律\left(f(t)越大,表明学生注意力越集中),经过实验分析得知: 
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,教师能否在学生达到所需的状态下讲授完这道题目?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,雾霾的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题,某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律,每生产该型号空气净化器![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)求利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 是以
是以![]() 为斜边的直角三角形,
为斜边的直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
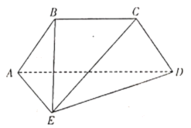
(1)若线段![]() 上有一个点
上有一个点![]() ,使得
,使得![]() 平面
平面![]() ,请确定点
,请确定点![]() 的位置,并说明理由;
的位置,并说明理由;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用![]() 列联表,由计算得
列联表,由计算得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com