考点:函数的值域
专题:计算题,函数的性质及应用
分析:(1)化简f(x)=2x|x-4|=
| | -2x2+8x,3≤x≤4 | | 2x2-8x,4<x≤5 |
| |
,由二次函数的单调性可得f(x)的单调区间,从而求f(x)在区间[3,5]上的值域;
(2)由(1)知,?x
1∈[3,5],?x
2∈[3,5],使f(x
1)=g(x
2)可化为[0,10]⊆{g(x)|g(x)=
,a>0,x∈[3,5]},从而可得[-2,8]⊆{(x-1)+
|a>0,x∈[3,5]},从而得到即
,从而求解.
解答:
解:(1):f(x)=2x|x-4|=
| | -2x2+8x,3≤x≤4 | | 2x2-8x,4<x≤5 |
| |
,
故f(x)在[3,4]上单调递减,在[4,5]上单调递增,
则0≤f(x)≤2×5×1=10;
故f(x)在区间[3,5]上的值域为[0,10];
(2)∵f(x)在区间[3,5]上的值域为[0,10],
∴?x
1∈[3,5],?x
2∈[3,5],使f(x
1)=g(x
2)可化为
[0,10]⊆{g(x)|g(x)=
,a>0,x∈[3,5]},
∵g(x)=
=(x-1)+
+2,
∴[-2,8]⊆{(x-1)+
|a>0,x∈[3,5]};
则1-a<0,即a>1,
且当a>1时,h(x)=(x-1)+
在[3,5]上是增函数,
则上式可化为h(3)≤-2且h(5)≥8;
即
,
不等式组无解.
故不存在实数a.
点评:本题考查了分段函数的值域的求法及恒成立问题的处理方法,属于中档题.



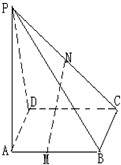 如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点;
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点;