
【题目】已知M,N是平面![]() 两侧的点,三棱锥
两侧的点,三棱锥![]() 所有棱长是2,
所有棱长是2,![]() ,
,![]() ,如图.
,如图.
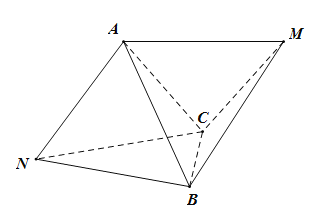
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦.
所成锐二面角的余弦.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取线段![]() 中点D,分别连结
中点D,分别连结![]() ,由平面几何的知识、线面垂直的判定
,由平面几何的知识、线面垂直的判定![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 与平面
与平面![]() 重合,再由平面几何的知识可得四边形
重合,再由平面几何的知识可得四边形![]() 是平行四边形,再由线面平行的判定即可得证;
是平行四边形,再由线面平行的判定即可得证;
(2)取线段![]() 的中点O,连结
的中点O,连结![]() ,建立空间直角坐标系,求出各点坐标,求出平面
,建立空间直角坐标系,求出各点坐标,求出平面![]() 的一个法向量
的一个法向量![]() 、平面
、平面![]() 的一个法向量
的一个法向量![]() ,再由
,再由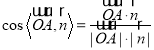 即可得解.
即可得解.
(1)证明:取线段![]() 中点D,分别连结
中点D,分别连结![]() ,
,
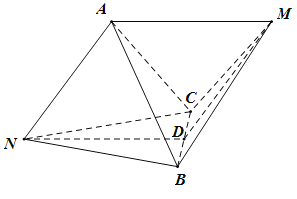
由条件得![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 与
与![]() 是平面
是平面![]() 内两相交直线,
内两相交直线,
![]() 与
与![]() 是平面
是平面![]() 内两相交直线,
内两相交直线,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 与平面
与平面![]() 重合,
重合,
![]()
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,即
是平行四边形,即![]() .
.
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ;
;
(2)取线段![]() 的中点O,连结
的中点O,连结![]() ,
,
由(1)知,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,
以过O平行![]() 的直线为x轴,分别以直线
的直线为x轴,分别以直线![]() 为y和z轴建立如图所示的空间直角坐标系
为y和z轴建立如图所示的空间直角坐标系![]() ,
,
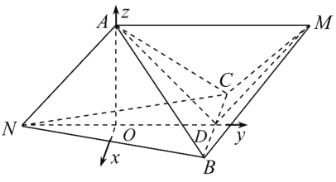
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
![]()
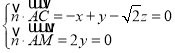 ,不妨取
,不妨取![]() ,得
,得![]() ,
,
又平面![]() 的一个法向量
的一个法向量![]() ,
,
![]()
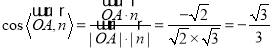 ,
,
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦为
所成锐二面角的余弦为![]() .
.


科目:高中数学 来源: 题型:
【题目】某校高一200名学生的期中考试语文成绩服从正态分布![]() ,数学成绩的频数分布直方图如下:
,数学成绩的频数分布直方图如下:

(I)计算这次考试的数学平均分,并比较语文和数学哪科的平均分较高(假设数学成绩在频率分布直方图中各段是均匀分布的);
(II)如果成绩大于85分的学生为优秀,这200名学生中本次考试语文、数学优秀的人数大约各多少人?
(III)如果语文和数学两科都优秀的共有4人,从(II)中的这些同学中随机抽取3人,设三人中两科都优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附参考公式)若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图,如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
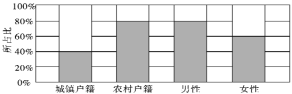
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人群中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在
,若存在![]() ,使
,使![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 型函数”;若存在
型函数”;若存在![]() ,使
,使![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 型函数”.已知函数
型函数”.已知函数![]() .
.
(1)设函数![]() .若
.若![]() ,且
,且![]() 为“
为“![]() 型函数”,求
型函数”,求![]() 的取值范围;
的取值范围;
(2)设函数![]() .证明:当
.证明:当![]() ,
,![]() 为“
为“![]() (1)型函数”;
(1)型函数”;
(3)若![]() ,证明存在唯一整数
,证明存在唯一整数![]() ,使得
,使得![]() 为“
为“![]() 型函数”.
型函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.
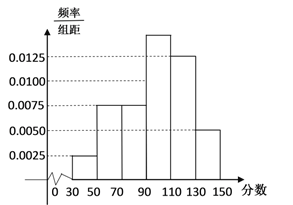
(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、…等标记来表示纸张的幅面规格.复印纸幅面规格只采用
、…等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中
系列,其中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 、
、![]() 、
、![]() 、…、
、…、![]() 所有规格的纸张的幅宽(以
所有规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系都为
表示)的比例关系都为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,
规格,![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的宽度为
纸的宽度为![]() ,则
,则![]() 纸的长度为______
纸的长度为______![]() ;
;![]() 、
、![]() 、…、
、…、![]() 八张纸的面积之和等于______
八张纸的面积之和等于______![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com