
分析 由已知得$\overrightarrow{a}•\overrightarrow{b}$=m+n-6=0,从而m+n=6,由此利用均值定理能求出mn的最大值.
解答 解:∵m>0,n>0,向量$\overrightarrow{a}$=(m,1,-3)与$\overrightarrow{b}$=(1,n,2)垂直,
∴$\overrightarrow{a}•\overrightarrow{b}$=m+n-6=0,即m+n=6,
∴mn≤($\frac{m+n}{2}$)2=9,
当且仅当m=n=3时,取等号,
∴mn的最大值为9.
故答案为:9.
点评 本题考查两数积的最大值的求法,是基础题,解题时要认真审题,注意向量垂直的性质和均值定理的合理运用.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 1或2 | D. | 1或-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧(¬q) | B. | (¬p)∧q | C. | (¬p)∧(¬q) | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
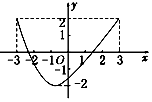
| A. | (-3,3),(-2,2) | B. | [-2,2],[-3,3] | C. | [-3,3],[-2,2] | D. | (-2,2),(-3,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com