
【题目】下列命题中不正确的是( )
A. 平面![]() ∥平面
∥平面![]() ,一条直线
,一条直线![]() 平行于平面
平行于平面![]() ,则
,则![]() 一定平行于平面
一定平行于平面![]()
B. 平面![]() ∥平面
∥平面![]() ,则
,则![]() 内的任意一条直线都平行于平面
内的任意一条直线都平行于平面![]()
C. 一个三角形有两条边所在的直线分别平行于一个平面,那么该三角形所在的平面与这个平面平行
D. 分别在两个平行平面内的两条直线只能是平行直线或异面直线
科目:高中数学 来源: 题型:
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.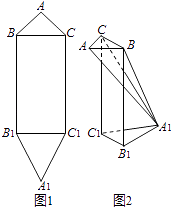
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() +k(
+k(![]() +lnx)(k为常数).
+lnx)(k为常数).
(1)当k=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当k≥0时,求函数f(x)的单调区间;
(3)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.
(1)求x和y的值;
(2)从成绩在90分以上的学生中随机取两名学生,求甲组至少有一名学生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半径为1的圆O内切于正方形ABCD,正六边形EFGHPR内接于圆O,当EFGHPR绕圆心O旋转时,![]()
![]() 的取值范围是( )
的取值范围是( )
A.[1﹣![]() , 1+
, 1+![]() ]
]
B.[﹣1-![]() , ﹣1+
, ﹣1+![]() ]
]
C.[![]() ﹣
﹣![]() ,
, ![]() +
+![]() ]
]
D.[-![]() ﹣
﹣![]() , -
, -![]() +
+![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的外接圆半径
的外接圆半径![]() ,角A、B、C的对边分别是a、b、c,且
,角A、B、C的对边分别是a、b、c,且![]() .
.
(I)求角B和边长b;
(II)求![]() 面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 |
|
|
|
|
该公司从注册的会员中,随机抽取了![]() 位进行统计,得到统计数据如下:
位进行统计,得到统计数据如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 |
|
|
|
|
|
假设汽车美容一次,公司成本为![]() 元.根据所给数据,解答下列问题:
元.根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)该公司从至少消费两次的顾客中按消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品.求抽出的2人中恰有1人消费两次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cos θ.
(1)求出圆C的直角坐标方程;
(2)已知圆C与x轴相交于A,B两点,直线l:y=2x关于点M(0,m)(m≠0)对称的直线为l′.若直线l′上存在点P使得∠APB=90°,求实数m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com