
【题目】已知若干个长方体盒子,其棱长均为不大于正奇数![]() 的正整数(允许三棱长相同),且盒壁厚度忽略不计,每个盒子的三组对面分别染为红、蓝、黄三色,若没有一个盒子能以同色面平行的方式装入另一个盒子中,则称这些盒子是“和谐的”,求最多有多少个和谐盒子?
的正整数(允许三棱长相同),且盒壁厚度忽略不计,每个盒子的三组对面分别染为红、蓝、黄三色,若没有一个盒子能以同色面平行的方式装入另一个盒子中,则称这些盒子是“和谐的”,求最多有多少个和谐盒子?
【答案】![]()
【解析】
设和谐盒子最多有![]() 个,在空间直角坐标系中,坐标面
个,在空间直角坐标系中,坐标面![]() ,
,![]() ,
,![]() 分别染为红、蓝、黄三色,将上述盒子放入坐标系中,使其共顶点的三面分别放入同色的坐标面中,则每个盒子与一个整数有序数组
分别染为红、蓝、黄三色,将上述盒子放入坐标系中,使其共顶点的三面分别放入同色的坐标面中,则每个盒子与一个整数有序数组![]() 一一对应,其中,
一一对应,其中,![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() .从而,和谐盒子集合对应一个空间直角坐标系中的点集
.从而,和谐盒子集合对应一个空间直角坐标系中的点集![]() ,
,![]() ,满足对于任意
,满足对于任意![]() 中的两点
中的两点![]() ,
,![]() ,有
,有![]() , ①其中,
, ①其中,![]() .
.
设![]() ,其中,
,其中,![]() ,令
,令![]() ,
,![]() .显然,
.显然,![]() 中任意两点至多有一个分量相同,即
中任意两点至多有一个分量相同,即![]() ,且对任意
,且对任意![]() ,
,![]() ,有
,有![]() . ②
. ②
将![]() 中各元按
中各元按![]() 分量的大小排序,记为
分量的大小排序,记为![]() ,其中,
,其中,![]() .由式①知
.由式①知![]() .故
.故![]() ,如图,在
,如图,在![]() 坐标平面内记
坐标平面内记![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,
,![]() ,
,![]() .从而,式②等价于
.从而,式②等价于![]() . ③
. ③
对于![]() ,若
,若![]() ,则将所有
,则将所有![]() 中的点并入
中的点并入![]() 中,将新集合记为
中,将新集合记为![]() ,则
,则![]() 仍满足式③,对
仍满足式③,对![]() 继续上述调整,直至
继续上述调整,直至![]() ,此时,仍记为
,此时,仍记为![]() ,将
,将![]() 各点依次连成一条折线,则所有
各点依次连成一条折线,则所有![]() 组成
组成![]() 中互不相交
中互不相交![]() 条折线,故
条折线,故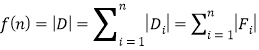
![]()
![]() ,当
,当![]() ,即
,即![]() 时,上式等号成立.
时,上式等号成立.
综上,和谐盒子至多有![]() 个.
个.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】某市教学研究室为了对今后所出试题的难度有更好的把握,提高命题质量,对该市高三理科数学试卷的得分情况进行了调研.从全市参加考试的理科考生中随机抽取了100名考生的数学成绩(满分150分),将数据分成9组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差
,并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差![]() ,以频率值作为概率估计值.
,以频率值作为概率估计值.
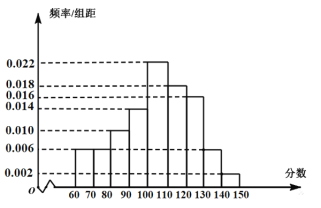
(Ⅰ)根据频率分布直方图,求抽取的100名理科考生数学成绩的平均分![]() 及众数
及众数![]() ;
;
(Ⅱ)用频率估计概率,从该市所有高三理科考生的数学成绩中随机抽取3个,记理科数学成绩位于区间![]() 内的个数为
内的个数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)从该市高三理科数学考试成绩中任意抽取一份,记其成绩为![]() ,依据以下不等式评判(
,依据以下不等式评判(![]() 表示对应事件的概率):
表示对应事件的概率):
①![]() ,②
,②![]() ,
,
③![]() ,其中
,其中![]() .
.
评判规则:若至少满足以上两个不等式,则给予这套试卷好评,否则差评.试问:这套试卷得到好评还是差评?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .将曲线
.将曲线![]() 上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线
上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为鼓励应届毕业大学生自主创业,国家对应届毕业大学生创业贷款有贴息优惠政策,现有应届毕业大学生甲贷款开小型超市,初期投入为72万元,经营后每年的总收入为50万元,该公司第![]() 年需要付出的超市维护和工人工资等费用为
年需要付出的超市维护和工人工资等费用为![]() 万元,已知
万元,已知![]() 为等差数列,相关信息如图所示.
为等差数列,相关信息如图所示.

(Ⅰ)求![]() ;
;
(Ⅱ)该超市第几年开始盈利?(即总收入减去成本及所有费用之差为正值)
(Ⅲ)该超市经营多少年,其年平均获利最大?最大值是多少?(年平均获利![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考虑![]() 的方格表,其中每个方格内均填有数字0.每次操作可先选定三个实数
的方格表,其中每个方格内均填有数字0.每次操作可先选定三个实数![]() 、
、![]() 、
、![]() ,然后选定一行,将这一行每个方格中的数都加上
,然后选定一行,将这一行每个方格中的数都加上![]() (
(![]() 为该方格所在的列数,
为该方格所在的列数,![]() );或选定一列,将这一列每个方格中的数都加上
);或选定一列,将这一列每个方格中的数都加上![]() (
(![]() 为该方格所在的行数,
为该方格所在的行数,![]() ),问:能否经过有限次操作,使该方格表中四个角的数字变成1,而其他格的数字仍为0?
),问:能否经过有限次操作,使该方格表中四个角的数字变成1,而其他格的数字仍为0?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 方格表的每个方格任意填入
方格表的每个方格任意填入![]() 或
或![]() ,然后允许进行如下操作:每次任意选择一行(或列),将这一行(或列)中的数全部变号.若无论开始时方格表的数怎样填,总能经过不超过
,然后允许进行如下操作:每次任意选择一行(或列),将这一行(或列)中的数全部变号.若无论开始时方格表的数怎样填,总能经过不超过![]() 次操作,使得方格表每一行中所有数的和、每一列中所有数的和均非负.试确定
次操作,使得方格表每一行中所有数的和、每一列中所有数的和均非负.试确定![]() 的最小值
的最小值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击新冠病毒,某部门安排甲、乙、丙、丁、戊五名专家到三地指导防疫工作.因工作需要,每地至少需安排一名专家,其中甲、乙两名专家必须安排在同一地工作,丙、丁两名专家不能安排在同一地工作,则不同的分配方法总数为( )
A.18B.24C.30D.36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com