
分析 通过题意得出关系式y=900(x+$\frac{16}{x}$)+5800(0<x≤5),利用基本不等式可知x+$\frac{16}{x}$≥8(当且仅当x=4时取等号),进而计算可得结论.
解答 解:由题可知y=3(2x×150+$\frac{12}{x}$×400)+5800
=900(x+$\frac{16}{x}$)+5800(0<x≤5),
∵x+$\frac{16}{x}$≥2$\sqrt{x•\frac{16}{x}}$=8,当且仅当x=$\frac{16}{x}$即x=4时取等号,
∴y=900(x+$\frac{16}{x}$)+5800在x=4时取最小值900×8+5800=13000,
于是当侧面的长度为4米时,总造价最底.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,利用基本不等式是解决本题的关键,注意解题方法的积累,属于基础题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
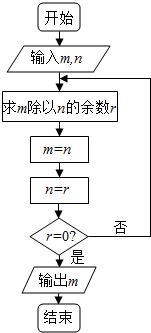 如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )
如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )| A. | 0 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$或0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com