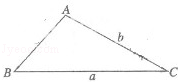
试题分析:先利用数学语言准确叙述出余弦定理的内容,并画出图形,写出已知与求证,然后开始证明.
方法一:采用向量法证明,由a的平方等于
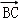
的平方,利用向量的三角形法则,由
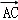
﹣
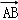
表示出
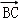
,然后利用平面向量的数量积的运算法则化简后,即可得到a
2=b
2+c
2﹣2bccosA,同理可证b
2=c
2+a
2﹣2cacosB,c
2=a
2+b
2﹣2abcosC;
方法二:采用坐标法证明,方法是以A为原点,AB所在的直线为x轴建立平面直角坐标系,表示出点C和点B的坐标,利用两点间的距离公式表示出|BC|的平方,化简后即可得到a
2=b
2+c
2﹣2bccosA,同理可证b
2=c
2+a
2﹣2cacosB,c
2=a
2+b
2﹣2abcosC.
解:余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍;或在△ABC中,a,b,c为A,B,C的对边,有a
2=b
2+c
2﹣2bccosA,b
2=c
2+a
2﹣2cacosB,c
2=a
2+b
2﹣2abcosC.
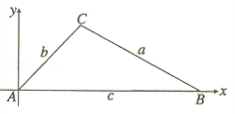
证法一:如图,
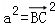
=

=
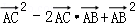
=
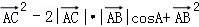
=b
2﹣2bccosA+c
2即a
2=b
2+c
2﹣2bccosA
同理可证b
2=c
2+a
2﹣2cacosB,c
2=a
2+b
2﹣2abcosC;
证法二:已知△ABC中A,B,C所对边分别为a,b,c,以A为原点,AB所在直线为x轴建立直角坐标系,
则C(bcosA,bsinA),B(c,0),
∴a
2=|BC|
2=(bcosA﹣c)
2+(bsinA)
2=b
2cos
2A﹣2bccosA+c
2+b
2sin
2A=b
2+c
2﹣2bccosA,
同理可证b
2=a
2+c
2﹣2accosB,c
2=a
2+b
2﹣2abcosC.
点评:此题考查学生会利用向量法和坐标法证明余弦定理,以及对命题形式出现的证明题,要写出已知求证再进行证明,是一道基础题.

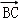 的平方,利用向量的三角形法则,由
的平方,利用向量的三角形法则,由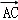 ﹣
﹣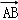 表示出
表示出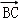 ,然后利用平面向量的数量积的运算法则化简后,即可得到a2=b2+c2﹣2bccosA,同理可证b2=c2+a2﹣2cacosB,c2=a2+b2﹣2abcosC;
,然后利用平面向量的数量积的运算法则化简后,即可得到a2=b2+c2﹣2bccosA,同理可证b2=c2+a2﹣2cacosB,c2=a2+b2﹣2abcosC;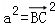 =
= =
=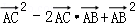
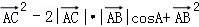 =b2﹣2bccosA+c2
=b2﹣2bccosA+c2



 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量 ,
, ,且
,且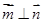 .
.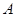 的大小;
的大小;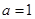 ;②
;② ;③
;③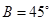 ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定 ,求出所确定的
,求出所确定的 的面积.
的面积.