
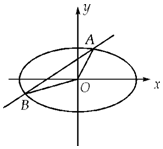
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列,记△AOB的面积为S.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列,记△AOB的面积为S.分析 (1)根据椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,建立方程,求出几何量,即可求椭圆C的方程.
(2)设直线l的方程为y=kx+m,代入椭圆方程,消去y,根据k1、k、k2恰好构成等比数列,求出k,进而表示出|OA|2+|OB|2,即可得出结论;
(3)表示出△ABO的面积,利用基本不等式,即可求S的最大值.
解答 解:(1)由题意可知a=2b且$\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}=1$,∴a=2,b=1,∴椭圆C的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),
由直线l的方程代入椭圆方程,消去y得:(1+4k2)x2+8kmx+4m2-4=0,
∴x1+x2=-$\frac{8km}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$,且△=16(1+4k2-m2)>0,
∵k1、k、k2恰好构成等比数列.
∴k2=k1k2=$\frac{(k{x}_{1}+m)(k{x}_{2}+m)}{{x}_{1}{x}_{2}}$.
∴-4k2m2+m2=0,∴k=±$\frac{1}{2}$.
∴x1+x2=±2m,x1x2=2m2-2
∴|OA|2+|OB|2=x12+y12+x22+y22=$\frac{3}{4}$[(x1+x2)2-2x1x2]+2=5,
∴|OA|2+|OB|2是定值为5.
(3))S=$\frac{1}{2}$|AB|d=$\frac{1}{2}\sqrt{1+{k}^{2}•}|{x}_{1}-{x}_{2}\\;|•\\;\frac{|\\;m\\;|\\;\\;\\;}{\sqrt{1+{k}^{2}}}$=$\sqrt{(2-{m}^{2}){m}^{2}}≤\sqrt{(\frac{2-{m}^{2}+{m}^{2}}{2}})^{2}=1$.
当且仅当m=±1时,S的最大值为1.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,等比数列的性质,基本不等式,考查学生分析解决问题的能力,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 若一个命题的逆命题是真命题,则它的否命题一定是真命题 | |
| B. | 若一个命题的逆命题是真命题,则它的逆否命题一定是真命题 | |
| C. | 若一个命题的逆命题是真命题,则它的否命题一定是假命题 | |
| D. | 若一个命题的逆命题是真命题,则它的逆否命题一定是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
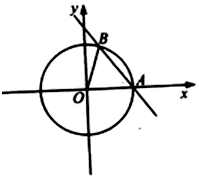 已知:如图所示,直线AB:$\sqrt{3}x+y-2\sqrt{3}=0$与圆O:x2+y2=4相交于点A,B,求证:△AOB是等边三角形.
已知:如图所示,直线AB:$\sqrt{3}x+y-2\sqrt{3}=0$与圆O:x2+y2=4相交于点A,B,求证:△AOB是等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com