分析:(1)由图形及题设条件知可证A1C1⊥B1D1,B1E⊥AC1,从而得出AC1⊥平面B1D1E.
(2)建立空间坐标系,求出两个平面的法向量,若两平面垂直则法向量内积为0,利用此方程求参数,若能求出则存在,否则不存在,解答本题时注意答题格式.
解答:(1)证明:连接A
1C
1,因为棱柱ABCD-A
1B
1C
1D
1是正四棱柱,所以A
1C
1⊥B
1D
1,
又A
1C
1是AC
1在底面A
1B
1C
1D
1内的射影,因此B
1D
1⊥AC
1,(2分)
同理,BC
1是AC
1在平面BCC
1B
1内的射影,
因为B
1E⊥BC
1,所以B
1E⊥AC
1,
又B
1D
1∩B
1E=B
1,所以AC
1⊥平面B
1D
1E(3分)
(2)解:存在实数λ,使得平面AD
1E⊥平面B
1D
1E,证明如下:
因为
=λ,所以
EC1=,因为
AB=BC=AA1,
不妨设AB=1,则AA
1=2,以D
1为坐标原点,分别以D
1A
1,D
1C
1,D
1D为x,y,z轴建立坐标系,
则
=(1,1,0),=(1,0,2),=(0,1,),(2分)
设平面AD
1E的一个法向量为n
1,由
得一个
n1=(2,,-1),
同理得平面D
1B
1E的一个法向量
n2=(1,-1,),(3分)
令n
1•n
2=0,即
2×1+×(-1)+(-1)×=0,
解得λ=1,
所以存在实数λ=1,使得平面AD
1E⊥平面B
1D
1E(2分)
点评:考查线面垂直的证明以及利用面面垂直建立相应的方程求参数,其中由位置关系建立方程求参数的题型类似于代数的选定系数法,先引入参数,建立相应等量关系,再解方程求出根,以确定相应的位置关系是否存在.

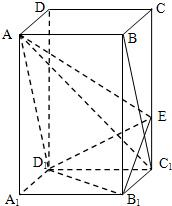 如图,在正四棱柱ABCD-A1B1C1D1中,AB=BC=
如图,在正四棱柱ABCD-A1B1C1D1中,AB=BC=

 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点. 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′= (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1= 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )