
����Ŀ��������Ϊ�˶Ա���ѧ���Ŀ��Գɼ����з����������ӱ���24��Ůͬѧ��18����ͬѧ�������ȡһ������Ϊ7���������з���.
��1����������Ա�����ֲ�������ɵõ����ٸ���ͬ����������д����ʽ���ɣ����ؼ���������
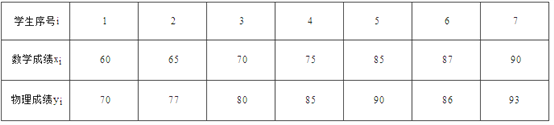
��2����������ȡ��7��ͬѧ����ѧ�������ɼ�����λ���֣���Ӧ���±���
���涨85�����ϣ�����85�֣�Ϊ���㣬����7��ͬѧ�г�ȡ3��ͬѧ����3��ͬѧ����ѧ�������ɼ���Ϊ���������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
���𰸡���1����ͬ�������ĸ���Ϊ![]() ��2���ֲ��м�������
��2���ֲ��м������� ![]()
![]()
���������������������1�����������������÷ֲ�����ķ����ֱ������ŮͬѧӦ�ó�ȡ��������3��4���������������ʽ���ֲ�����ԭ�������ȡ�����ĸ�������2������������ֱ����![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ����д�����ʷֲ��У�����������ѧ������ʽ�������ѧ������
����д�����ʷֲ��У�����������ѧ������ʽ�������ѧ������
�⣺(1)���ݷֲ�����ķ����� ![]() ��Ůͬѧ��Ӧ��ȡ������Ϊ
��Ůͬѧ��Ӧ��ȡ������Ϊ![]() ����
����
![]() ����ͬѧ��Ӧ��ȡ������Ϊ
����ͬѧ��Ӧ��ȡ������Ϊ![]() ����
����
�ʲ�ͬ�������ĸ���Ϊ![]() .
.
(2)��![]() ��ͬѧ����ѧ�������ɼ���Ϊ���������Ϊ
��ͬѧ����ѧ�������ɼ���Ϊ���������Ϊ![]() ��,
��,
��![]() ��ȡֵΪ
��ȡֵΪ![]()
��![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() .
.
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
|
|
��![]()
![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij��λ��ְ��ʳ���У�ʳ��ÿ����![]() Ԫ/���ļ۸������깺�������Ȼ����
Ԫ/���ļ۸������깺�������Ȼ����![]() Ԫ/���ļ۸���ۣ�������������꣬ʣ�µ������
Ԫ/���ļ۸���ۣ�������������꣬ʣ�µ������![]() Ԫ/���ļ۸��������ϼӹ�������������ͳ�����ϣ��õ�ʳ��ÿ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��ʳ��ij�칺����90���������
Ԫ/���ļ۸��������ϼӹ�������������ͳ�����ϣ��õ�ʳ��ÿ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��ʳ��ij�칺����90���������![]() ����λ������
����λ������ ![]() ����ʾ�������������
����ʾ������������� ![]() ����λ��Ԫ����ʾ����
����λ��Ԫ����ʾ����

������![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
������ֱ��ͼ��������![]() ������
������![]() Ԫ�ĸ��ʣ�
Ԫ�ĸ��ʣ�
��III����ֱ��ͼ�������������У��Ը���������е�ֵ��������ĸ���ֵ����������������������Ƶ����Ϊ������ȡ�������м�ֵ�ĸ���(���磺��������![]() ����ȡ
����ȡ![]() ����
����![]() �ĸ��ʵ�������������
�ĸ��ʵ�������������![]() ��Ƶ��)����
��Ƶ��)����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������������
��������������
������![]() ����ͼ������ƽ��
����ͼ������ƽ��![]() ����λ���Ⱥ����
����λ���Ⱥ����![]() ��Գƣ���
��Գƣ���![]() .
.
��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ι���ѧ�������ϣ������ĸ����ҵ���λ��������������һ��Բ����Ϊ��ʹ�����ܹ����ɽ�̸�������˽��������£�
�����й��ˣ�����˵Ӣ�
���Ƿ����ˣ�����˵���
����Ӣ���ˣ�����˵���
�����ձ��ˣ�����˵���
���Ƿ����ˣ�����˵���
������λ��������λ˳��ӦΪ�� ��
A. �ױ������� B. ��������
C. ���ұ����� D. �ױ����Ҷ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1������![]() ��ͼ����
��ͼ����![]() �������߷��̣�
�������߷��̣�
��2���Ƿ����ʵ��![]() ��ʹ�ö������
��ʹ�ö������![]() �����к���
�����к���![]() ��ͼ����
��ͼ����![]() ��ͼ����·��������ڣ������������
��ͼ����·��������ڣ������������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���ο����ݣ� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
��1����![]() �����ۺ���
�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2���Ƿ����ʵ��![]() ��������
��������![]() ��
�� ![]() �� ��
�� ��![]() ������������ڣ����
������������ڣ����![]() �ķ�Χ���������ڣ���˵�����ɣ�
�ķ�Χ���������ڣ���˵�����ɣ�
��3����![]() �����
�����![]() �Ǻ���
�Ǻ���![]() ��������㣬��
��������㣬��![]() ��
�� ![]() ��
��![]() �ĵ�������֤����
�ĵ�������֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ����ֱ֪��
���������Ϊ���Ὠ��������ϵ����ֱ֪��![]() ������
������![]() �ļ�����ֱ�Ϊ
�ļ�����ֱ�Ϊ ��Բ
��Բ![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() ��������
��������
��1����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��ֱ��
���е㣬��ֱ��![]() ��ƽ��ֱ�����귽�̣�
��ƽ��ֱ�����귽�̣�
��2���ж�ֱ��![]() ��Բ
��Բ![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��
�� ![]() +3����1��x��2����
+3����1��x��2����
��1������= ![]() ʱ������f��x����ֵ��
ʱ������f��x����ֵ��
��2��������f��x������Сֵ��1����ʵ���˵�ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com