
【题目】圆M:x2+y2﹣2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1 , l2 , 切点为B,C. 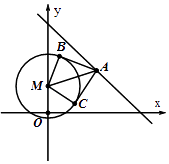
(1)当a=0时,求直线l1 , l2的方程;
(2)是否存在点A,使得 ![]() =﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
=﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
(3)求证当点A在直线l运动时,直线BC过定点P0 .
(附加题)问:第(3)问的逆命题是否成立?
【答案】
(1)解:圆M:x2+(y﹣1)2=25,圆心M(0,1),半径r=5,A(0,11),
设切线的方程为y=k x+11,圆心距d= ![]() =5,
=5,
∴k=± ![]() ,所求直线l1,l2的方程为y=±
,所求直线l1,l2的方程为y=± ![]() x+11
x+11
(2)解:当l1⊥l2时,四边形MCAB为正方形,
∴|AM|+ ![]() |MB|=5
|MB|=5 ![]()
设A(a,11﹣a),M(0,1)则 ![]() =
= ![]()
a2﹣10a+25=0∴a=5
设 ![]() =2θ,则
=2θ,则
![]() =|AB|2(1﹣2sin2θ),
=|AB|2(1﹣2sin2θ),
又sinθ= ![]() ,故
,故 ![]() =(AM2﹣25)(1﹣
=(AM2﹣25)(1﹣ ![]() )=AM2+
)=AM2+ ![]() ﹣75,
﹣75,
又圆心M到直线l的距离是 ![]()
∴AM2≥50, ![]() ≥50+
≥50+ ![]() ﹣75=0,故点A不存在.
﹣75=0,故点A不存在.
(3)解:设A(a,b),则a+b=1 ①;
已AM为直径的圆与圆M交于B,C,AB,AC为切线;
以AM为直径的圆方程为:x(x﹣a)+(y﹣1)(y﹣b)=0 ②
圆M:x2+y2﹣2y=24 ③,
两式②③相减得公共弦BC方程:24+2y﹣ax﹣(b+1)y+b=0,代入①化简:
y﹣ ![]() =﹣
=﹣ ![]() (x﹣
(x﹣ ![]() ),故知P0 (
),故知P0 ( ![]() ,
, ![]() ).
).
附加题:
首先:第(3)的逆命题是:过定点P0 ( ![]() ,
, ![]() )的直线交圆x2+y2﹣2y=24 于B.C两点,分别以B,C为切点作圆M的切线l1,l2 相交于A点,则A在x+y=11上.
)的直线交圆x2+y2﹣2y=24 于B.C两点,分别以B,C为切点作圆M的切线l1,l2 相交于A点,则A在x+y=11上.
证明:设A(a,b),已AM为直径的圆与圆M交于B,C,易证AB,AC为切线;
以AM为直径的圆方程为:x(x﹣a)+(y﹣1)(y﹣b)=0
圆M:x2+y2﹣2y=24,
两式相减得公共弦BC方程:24+2y﹣ax﹣(b+1)y+b=0,
由于公共弦BC所在直线过定点P0 ( ![]() ,
, ![]() ),代入可得a+b=11,得证
),代入可得a+b=11,得证
【解析】(1)利用点到直线的距离公式,可直接求出斜率;(2)当l1⊥l2时,四边形MCAB为正方形,求出a的值;设 ![]() =2θ,则
=2θ,则 ![]() =|AB|2(1﹣2sin2θ),故
=|AB|2(1﹣2sin2θ),故 ![]() =(AM2﹣25)(1﹣
=(AM2﹣25)(1﹣ ![]() )=AM2+
)=AM2+ ![]() ﹣75,又圆心M到直线l的距离是
﹣75,又圆心M到直线l的距离是 ![]() ∴AM2≥50,
∴AM2≥50, ![]() ≥50+
≥50+ ![]() ﹣75=0,故点A不存在.(3)利用两圆方程相减,求出公共弦直线方程,找出定点.
﹣75=0,故点A不存在.(3)利用两圆方程相减,求出公共弦直线方程,找出定点.


科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,∠A是锐角,且 ![]() b=2asinB.
b=2asinB.
(1)求∠A的度数;
(2)若a=7,△ABC的面积为10 ![]() ,求b2+c2的值.
,求b2+c2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中内角A,B,C的对边分别为a,b,c,向量 ![]() =(2sinB,﹣
=(2sinB,﹣ ![]() ),
), ![]() =(cos2B,2cos2
=(cos2B,2cos2 ![]() ﹣1)且
﹣1)且 ![]() ∥
∥ ![]() .
.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1 , 且AA1=AB=2. 
(1)求证:AB⊥BC;
(2)若直线AC与平面A1BC所成的角为 ![]() ,求锐二面角A﹣A1C﹣B的大小.
,求锐二面角A﹣A1C﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图. 
(1)求分数在[70,80)内的频率;
(2)根据频率分布直方图,估计该校高一年级学生期中考试数学成绩的平均分;
(3)用分层抽样的方法在80分以上的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com