
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然常数.
是自然常数.
(1)判断函数![]() 在
在![]() 内零点的个数,并说明理由;
内零点的个数,并说明理由;
(2)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围.
的取值范围.
【答案】(1) 存在1个零点;理由见解析.
(2) ![]() .
.
【解析】分析:(1)![]() 在
在![]() 内零点的个数1,求得
内零点的个数1,求得![]() 的导数,判断符号,可得单调性,再由函数零点存在定理,即可得到结论;
的导数,判断符号,可得单调性,再由函数零点存在定理,即可得到结论;
(2)由题意可得![]() ,即
,即![]() ,分别求得
,分别求得![]() 在
在![]() 上的单调性,可得最值,解
上的单调性,可得最值,解![]() 的不等式,即可得到所求范围.
的不等式,即可得到所求范围.
详解:
(1)函数![]() 在
在![]() 上的零点的个数为1,理由如下:
上的零点的个数为1,理由如下:
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,
,![]() ,
,
根据函数零点存在性定理得函数![]() 在
在![]() 上存在1个零点.
上存在1个零点.
(2)因为不等式![]() 等价于
等价于![]() ,
,
所以![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,等价于
成立,等价于
![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,又
,又![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
因此,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
甲班 | 6 | 5 | 7 | 9 | 8 |
乙班 | 4 | 8 | 9 | 7 | 7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)在本次训练中,从两班中分别任选一个同学,比较两人的投中次数,求甲班同学投中次数高于乙班同学投中次数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
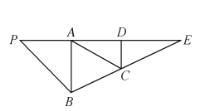
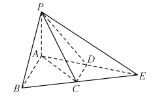
【题目】如图,在![]() 中,
中,![]() ,D是AE的中点,C是线段BE上的一点,且
,D是AE的中点,C是线段BE上的一点,且![]() ,
,![]() ,将
,将![]() 沿AB折起使得二面角
沿AB折起使得二面角![]() 是直二面角.
是直二面角.
(l)求证:CD平面PAB;
(2)求直线PE与平面PCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,中心在坐标原点,抛物线
轴上,中心在坐标原点,抛物线![]() 的焦点在
的焦点在![]() 轴上,顶点在坐标原点,在
轴上,顶点在坐标原点,在![]() 、
、![]() 上各取两个点,将其坐标记录于表格中:
上各取两个点,将其坐标记录于表格中:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 、
、![]() 的标准方程;
的标准方程;
(2)已知定点![]() ,
,![]() 为抛物线
为抛物线![]() 上的一点,其横坐标为
上的一点,其横坐标为![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线交椭圆
处的切线交椭圆![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 面积.
面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程ay=b2x2+c中的a,b,c∈{﹣3,﹣2,0,1,2,3},且a,b,c互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )
A.60条
B.62条
C.71条
D.80条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 在数列|![]() 中,
中,![]() 由此归纳出
由此归纳出![]() 的通项公式
的通项公式
B. 由平面三角形的性质,推测空间四面体性质
C. 某校高二共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人
D. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 . 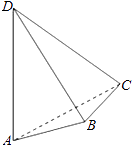
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com