
【题目】已知椭圆![]() 的离心率
的离心率![]() ,右焦点
,右焦点![]() ,过点
,过点 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:
,求证: ![]() 三点共线;
三点共线;
(3) 当![]() 面积最大时,求直线
面积最大时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)见解析;(3)
;(2)见解析;(3) ![]() .
.
【解析】试题分析:(1)根据离心率可求得![]() 的值,从而可求得
的值,从而可求得![]() 的值,进而可得结果;(2) 设
的值,进而可得结果;(2) 设![]() ,只需用平面向量坐标法证明
,只需用平面向量坐标法证明![]() 即可得结论;(3)设直线
即可得结论;(3)设直线![]() 的方程为
的方程为![]() ,根据韦达定理、弦长公式、三角形面积公式将
,根据韦达定理、弦长公式、三角形面积公式将![]() 面积表示为关于
面积表示为关于![]() 的函数式,换元后根据配方法求最值,取得最值时可以确定
的函数式,换元后根据配方法求最值,取得最值时可以确定![]() 的值,进而可得结果.
的值,进而可得结果.
试题解析:(1) 由![]() ,
, ![]() 椭圆
椭圆![]() 的方程是
的方程是![]() .
.
(2)由(1)可得![]() ,设直线
,设直线![]() 的方程为
的方程为![]() . 由方程组
. 由方程组 ,得
,得![]() ,依题意
,依题意![]() ,
,
得![]() .设
.设![]() ,则
,则![]() ,由
,由![]()
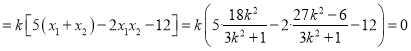 ,得
,得![]() 三点共线.
三点共线.
(3)设直线![]() 的方程为
的方程为![]() . 由方程组
. 由方程组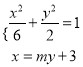 ,得
,得![]() ,依题意
,依题意![]() ,得
,得![]() .设
.设![]() ,则
,则![]()
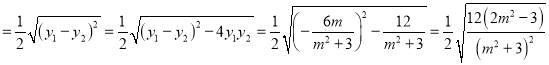 ,令
,令![]() ,则
,则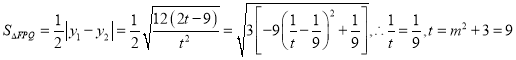 ,即
,即
![]() 时,
时, ![]() 最大,
最大, ![]() 最大时直线
最大时直线![]() 的方程为
的方程为![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用配方法法求三角形最值的.


科目:高中数学 来源: 题型:
【题目】已知 ![]() ,且方程
,且方程 ![]() 无实数根,下列命题:
无实数根,下列命题:
(1)方程 ![]() 一定有实数根;
一定有实数根;
(2)若 ![]() ,则不等式
,则不等式 ![]() 对一切实数
对一切实数 ![]() 都成立;
都成立;
(3)若 ![]() ,则必存在实数
,则必存在实数 ![]() ,使
,使 ![]() ;
;
(4)若 ![]() ,则不等式
,则不等式 ![]() 对一切实数
对一切实数 ![]() 都成立.
都成立.
其中,正确命题的序号是________________.(把你认为正确的命题的所有序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
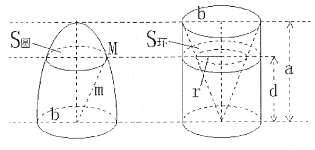
【题目】祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家. 他提出了一条原理:“幂势既同,則积不容异. ”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等. 该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年. 椭球体是椭圆绕其轴旋转所成的旋转体. 如图将底面直径皆为![]() ,高皆为
,高皆为![]() 的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面
的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面![]() 上. 以平行于平面
上. 以平行于平面![]() 的平面于距平面
的平面于距平面![]() 任意高
任意高![]() 处可横截得到
处可横截得到![]() 及
及![]() 两截面,可以证明
两截面,可以证明![]() 知总成立. 据此,短轴长为
知总成立. 据此,短轴长为![]() ,长轴为
,长轴为![]() 的椭球体的体积是 __________
的椭球体的体积是 __________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
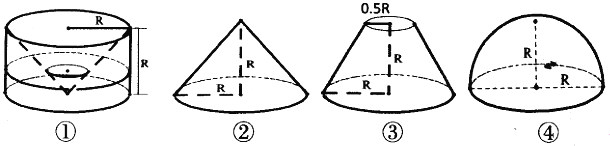
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片成熟森林的总面积为![]() (近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
(近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的![]() ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com