【题目】某运输公司接受了向一地区每天至少运送180 t物资的任务，该公司有8辆载重为6 t的A型卡车和4辆载重为10 t的B型卡车，有10名驾驶员，每辆卡车每天往返的次数为A型卡车4次，B型卡车3次，每辆卡车每天往返的费用为A型卡车320元，B型卡车504元，则公司如何调配车辆，才能使公司所花的费用最低，最低费用为________元.
科目：高中数学 来源： 题型：
【题目】已知椭圆
的上、下、左、右四个顶点分别为
x轴正半轴上的某点
满足
.
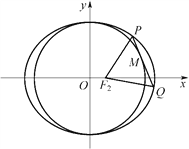
(1)求椭圆的方程;
(2)设该椭圆的左、右焦点分别为
,点
在圆
上,且
在第一象限,过
作圆
的切线交椭圆于
,求证:△
的周长是定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，五面体ABCDE，四边形ABDE是矩形，△ABC是正三角形，AB＝1，AE＝2，F是线段BC上一点，直线BC与平面ABD所成角为30°，CE∥平面ADF.
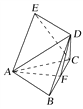
(1)试确定F的位置；
(2)求三棱锥A－CDF的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】园林管理处拟在公园某区域规划建设一半径为
米圆心角为
（弧度）的扇形景观水池，其中
为扇形
的圆心，同时紧贴水池周边建一圈理想的无宽度步道，要求总预算费用不超过
万元，水池造价为每平方米
元，步道造价为每米
元.
（1）当
和
分别为多少时，可使广场面积最大，并求出最大值；
（2）若要求步道长为
米，则可设计出水池最大面积是多少.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知AB是圆O的直径，C，D是圆上不同两点，且CD∩AB＝H，AC＝AD，PA⊥圆O所在平面．
(Ⅰ)求证：PB⊥CD；
(Ⅱ)若PB＝
，∠PBA＝
，∠CAD＝
，求H到平面PBD的距离．
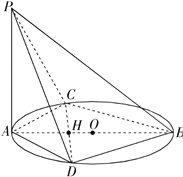
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，放置的边长为1的正方形PABC沿x轴滚动，点B恰好经过原点．设顶点P(x，y)的轨迹方程是y＝f(x)，则对函数y＝f(x)有下列判断：
①若－2≤x≤2，则函数y＝f(x)是偶函数；
②对任意的x∈R，都有f(x＋2)＝f(x－2)；
③函数y＝f(x)在区间[2,3]上单调递减；
④函数y＝f(x)在区间[4,6]上是减函数．
其中判断正确的序号是________．(写出所有正确结论的序号)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，正方体ABCD－A1B1C1D1中，E、F分别是AB和AA1的中点．
求证：(1)E、C、D1、F四点共面；
(2)CE、D1F、DA三线共点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的前n项和Sn，且3an＋Sn＝4(n∈N*).
(1)证明：{an}是等比数列；
(2)在an和an＋1之间插入n个数，使这n＋2个数成等差数列.记插入的n个数的和为Tn，求Tn的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
