
【题目】已知函数![]() .
.
(1)求![]() 的最大值;
的最大值;
(2)证明:对任意的![]() ,都有
,都有![]() ;
;
(3)设![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 上一点,
上一点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 满足
满足![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,是否存在定点
,是否存在定点![]() ,使得直线
,使得直线![]() 、
、![]() 的斜率之和恒为0.若存在,则求出点
的斜率之和恒为0.若存在,则求出点![]() 的坐标;若不存在,则请说明理由.
的坐标;若不存在,则请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度. 药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
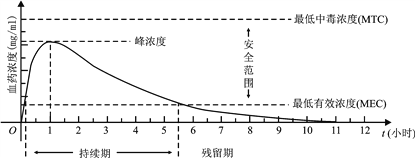
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是
A. 首次服用该药物1单位约10分钟后,药物发挥治疗作用
B. 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C. 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D. 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() φ)﹣cos(ωx+φ)(
φ)﹣cos(ωx+φ)(![]() ),x=0和x
),x=0和x![]() 是函数的y=f(x)图象的两条相邻对称轴.
是函数的y=f(x)图象的两条相邻对称轴.
(1)求f(![]() )的值;
)的值;
(2)将y=f(x)的图象向右平移![]() 个单位后,再将所得的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在[
个单位后,再将所得的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在[![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,定点
,定点![]() ,
,![]() 是圆
是圆![]() 上的一动点,线段
上的一动点,线段![]() 的垂直平分线交半径
的垂直平分线交半径![]() 于
于![]() 点.
点.
(1)求![]() 点的轨迹
点的轨迹![]() 的方程;
的方程;
(2)四边形![]() 的四个顶点都在曲线
的四个顶点都在曲线![]() 上,且对角线
上,且对角线![]() 、
、![]() 过原点
过原点![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②由变量![]() 和
和![]() 的数据得到其回归直线方程
的数据得到其回归直线方程![]() ,则
,则![]() 一定经过点
一定经过点![]() ;
;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
④将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
⑤在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.1个单位,
平均增加0.1个单位,
其中真命题的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com