
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且过点
,且过点![]() .直线
.直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最大值;
的面积的最大值;
(Ⅲ)设直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .判断
.判断![]() ,
, ![]() 大小关系,并加以证明.
大小关系,并加以证明.
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,![]() 为前
为前![]() 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则![]() _________________尺.
_________________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() ,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
(Ⅰ)求袋中原有白球的个数:
(Ⅱ)求取球次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:任意两个等边三角形都是相似的.
①它的否定是_________________________________________________________;
②否命题是_____________________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养;若
的值评定学生的数学核心素养;若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)函数![]() 在区间
在区间![]() 是单调函数,求实数
是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使得
,使得![]() 成立,求满足条件的最大整数
成立,求满足条件的最大整数![]() ;
;
(3)如果对任意的![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形PABC的各边及对角线长度都相等,D、E、F、G分别是AB、BC、CA、AP的中点,下列四个结论中成立的是
①BC∥平面PDF
②DF⊥平面PAE
③平面GDF∥平面PBC
④平面PAE⊥平面ABC.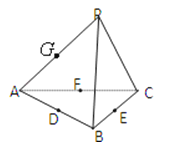
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com