
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,椭圆右顶点为
,椭圆右顶点为![]() ,点
,点![]() 在圆
在圆![]() :
:![]() 上.
上.
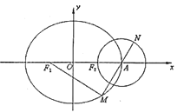
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 在椭圆
在椭圆![]() 上,且位于第四象限,点
上,且位于第四象限,点![]() 在圆
在圆![]() 上,且位于第一象限,已知
上,且位于第一象限,已知![]() ,求直线
,求直线![]() 的斜率.
的斜率.
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
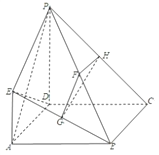
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以数列![]() 的任意相邻两项为坐标的点
的任意相邻两项为坐标的点![]() ,均在一次函数y=2x+k的图象上,数列
,均在一次函数y=2x+k的图象上,数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)求证数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的公比;
的公比;
(2)设数列![]() ,
,![]() 的前n项和分别为Sn,Tn,若S6=T4,S5=﹣9,求k的值.
的前n项和分别为Sn,Tn,若S6=T4,S5=﹣9,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读参考材料,再解决此问题:
参考材料:求抛物线弧![]() (
(![]() )与x轴及直线
)与x轴及直线![]() 所围成的封闭图形的面积
所围成的封闭图形的面积
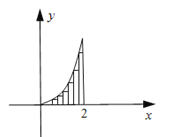
解:把区间![]() 进行n等分,得
进行n等分,得![]() 个分点
个分点![]() (
(![]() ),过分点
),过分点![]() ,作x轴的垂线,交抛物线于
,作x轴的垂线,交抛物线于![]() ,并如图构造
,并如图构造![]() 个矩形,先求出
个矩形,先求出![]() 个矩形的面积和
个矩形的面积和![]() ,再求
,再求![]() ,即是封闭图形的面积,又每个矩形的宽为
,即是封闭图形的面积,又每个矩形的宽为![]() ,第i个矩形的高为
,第i个矩形的高为![]() ,所以第i个矩形的面积为
,所以第i个矩形的面积为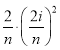 ;
;
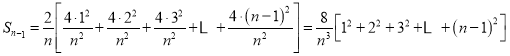
![]()
所以封闭图形的面积为![]()
阅读以上材料,并解决此问题:已知对任意大于4的正整数n,
不等式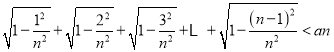 恒成立,
恒成立,
则实数a的取值范围为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,![]() 和
和![]() 都是正三角形,
都是正三角形,![]() , E、F分别是AC、BC的中点,且PD⊥AB于D.
, E、F分别是AC、BC的中点,且PD⊥AB于D.
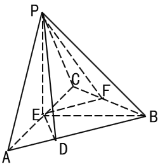
(Ⅰ)证明:直线![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()
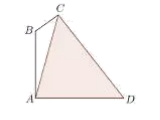
(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com