
【题目】已知f(x)=lnx+x2﹣bx.
(1)若函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当b=﹣1时,设g(x)=f(x)﹣2x2 , 求证函数g(x)只有一个零点.
【答案】
(1)解:∵f(x)在(0,+∞)上递增,
∴f′(x)= ![]() +2x﹣b≥0,对x∈(0,+∞)恒成立,即b≤
+2x﹣b≥0,对x∈(0,+∞)恒成立,即b≤ ![]() +2x对x∈(0,+∞)恒成立,
+2x对x∈(0,+∞)恒成立,
∴只需b≤( ![]() +2x)min (x>0),
+2x)min (x>0),
∵x>0,
∴ ![]() +2x≥2
+2x≥2 ![]() ,当且仅当x=
,当且仅当x= ![]() 时取“=”,∴b≤2
时取“=”,∴b≤2 ![]() ,
,
∴b的取值范围为(﹣∞,2 ![]() ]
]
(2)证明:当b=﹣1时,g(x)=f(x)﹣2x2=lnx﹣x2+x,其定义域是(0,+∞),
∴g′(x)= ![]() ﹣2x+1=﹣
﹣2x+1=﹣ ![]() ,
,
令g′(x)=0,∵x>0,∴x=1,
当0<x<1时,g′(x)>0;当x>1时,g′(x)<0,
∴函数g(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴当x≠1时,g(x)<g(1),即g(x)<0,当x=1时,g(x)=0.
∴函数g(x)只有一个零点
【解析】(1)其导函数,利用f(x)在(0,+∞)上递增,可得f′(x)≥0,对x∈(0,+∞)恒成立,分离参数,即可求得b的取值范围;(2)当b=﹣1时,g(x)=f(x)﹣2x2=lnx﹣x2+x,其定义域是(0,+∞),求导函数,确定合适的单调性,利用当x≠1时,g(x)<g(1),即g(x)<0,当x=1时,g(x)=0,即可得到结论.
【考点精析】解答此题的关键在于理解函数的极值的相关知识,掌握极值反映的是函数在某一点附近的大小情况.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.
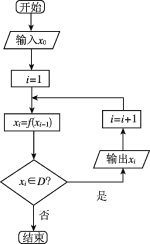
(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(9),f(27)的值
(2)解不等式f(x)+f(x﹣8)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种商品的经验表明,该商品每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为7元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为7元/千克时,每日可售出该商品11千克.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若该商品的成本为5元/千克,试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点). 
(1)求证:MN∥平面CDEF;
(2)求多面体A﹣CDEF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com