
【题目】下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.a=9,b=10,A=60°,无解
【答案】B
【解析】解:A、∵a=7,b=14,A=30°,
∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =1,
=1,
又B为三角形的内角,
∴B=90°,C=60°,c=7 ![]() ,
,
则此时三角形只有一解,此选项错误;
B、∵a=30,b=25,A=150°,
∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =
= ![]() ,
,
∵a>b,∴150°>A>B,
则此时B只有一解,本选项正确;
C、∵a=6,b=9,A=45°,
∴∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =
= ![]() >
> ![]() ,
,
∵b>a,∴B>A=45°,
∴此时B只有一解,本选项错误;
D、∵a=9,b=10,A=60°,
∴∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =
= ![]() >
> ![]() ,
,
∵a<b,∴60°=A<B,
此时B有两解,本选项错误,
故选B
【考点精析】利用正弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( ) 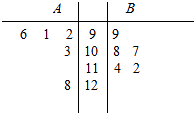
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点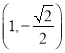 是椭圆
是椭圆![]() 上的点,离心率为
上的点,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 在椭圆上
在椭圆上![]() 上,若点
上,若点![]() 与点
与点![]() 关于原点的对称,连接
关于原点的对称,连接![]() ,并延长与椭圆
,并延长与椭圆![]() 的另一个交点为
的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x=1是函数f(x)=![]() ax3-
ax3-![]() x2+(a+1)x+5的一个极值点.
x2+(a+1)x+5的一个极值点.
(1)求函数f(x)的解析式;
(2)若曲线y=f(x)与直线y=2x+m有三个交点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0,且直线l与圆C交于A、B两点.
(1)若|AB|= ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P(1,1),满足2 ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,若sinA+sinB=sinC(cosA+cosB).
(1)判断△ABC的形状;
(2)在上述△ABC中,若角C的对边c=1,求该三角形内切圆半径的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16
(1)求数列{an}的通项公式;
(2)若a3 , a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记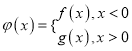 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式;
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com