
分析 同角三角函数的基本关系式把sinα用cosα表示出来.利用对数的运算法则化简计算即可.
解答 解:由lgsinα=lg($\sqrt{1-co{s}^{2}α}$)=$\frac{1}{2}$lg(1-cos2α)=$\frac{1}{2}$lg(1+cosα)+$\frac{1}{2}$lg(1-cosα)
∵lg(1+cosα)=m,$lg\frac{1}{1-cosα}=n$,即lg(1-cosα)=$\frac{1}{n}$
∴lgsinα=$\frac{1}{2}$m+$\frac{1}{2}$×$\frac{1}{n}$=$\frac{1}{2}$(m+$\frac{1}{n}$)
故答案为:$\frac{1}{2}$(m+$\frac{1}{n}$)
点评 此题考查了同角三角函数间的基本关系,熟练掌握同角三角函数的基本关系是解本题的关键.同时考查了对数的化简计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:选择题
已知a>0,b>0,且2a+b=ab,则a+2b的最小值为( )
A.5+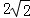 B.
B. C.5 D.9
C.5 D.9
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,2) | C. | (-∞,0) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
设数列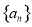 的前
的前 项和为
项和为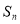 ,且
,且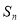
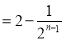 ,
,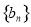 为等差数列,且
为等差数列,且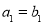 ,
,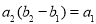 .
.
(1)求数列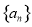 和
和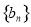 通项公式;
通项公式;
(2)设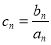 ,求数列
,求数列 的前
的前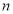 项和
项和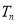 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,0) | C. | (-∞,0),(0,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{16}{5}$ | C. | 2$\sqrt{41}$ | D. | 164 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com