
【题目】某班从4位男生和3位女生志愿者选出4人参加校运会的点名签到工作,则选出的志愿者中既有男生又有女生的概率的是__________.(结果用最简分数表示)
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在R上的两个周期函数,
是定义在R上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
, ,其中k>0.若在区间(0,9]上,关于x的方程
,其中k>0.若在区间(0,9]上,关于x的方程![]() 有8个不同的实数根,则k的取值范围是_____.
有8个不同的实数根,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA.规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).

(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,圆
,圆![]() 为
为![]() .
.
(1)若椭圆![]() 的长轴为4,且焦距与椭圆
的长轴为4,且焦距与椭圆![]() 的焦距相等,求椭圆
的焦距相等,求椭圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 上任意一点
上任意一点![]() 作其切线
作其切线![]() ,若
,若![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求证:
两点,求证:![]() 为定值(
为定值(![]() 为坐标原点);
为坐标原点);
(3)在(2)的条件下,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果四面体的四条高交于一点,则该点称为四面体的垂心,该四面体称为垂心四面体.
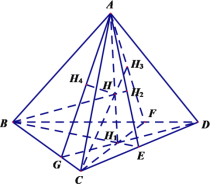
(1)证明:如果四面体的对棱互相垂直,则该四面体是垂心四面体;反之亦然.
(2)给出下列四面体
①正三棱锥;
②三条侧棱两两垂直;
③高在各面的射影过所在面的垂心;
④对棱的平方和相等.
其中是垂心四面体的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 为参数
为参数![]() ,圆C的标准方程为
,圆C的标准方程为![]() 以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
![]() 求直线l和圆C的极坐标方程;
求直线l和圆C的极坐标方程;
![]() 若射线
若射线![]() 与l的交点为M,与圆C的交点为A,B,且点M恰好为线段AB的中点,求a的值.
与l的交点为M,与圆C的交点为A,B,且点M恰好为线段AB的中点,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com