
【题目】如图所示,四棱锥![]() 中,
中,![]() 菱形
菱形![]() 所在的平面,
所在的平面,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 上的点.
上的点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,当
的中点,当![]() 时,是否存在点
时,是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 的所成角的正弦值为
的所成角的正弦值为![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

科目:高中数学 来源: 题型:
【题目】如图,已知图形ABCDEF,内部连有线段.
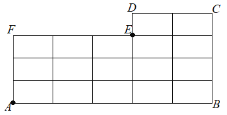
(1)由点A沿着图中的线段到达点E的最近路线有多少条?
(2)由点A沿着图中的线段到达点C的最近路线有多少条?
(3)求出图中总计有多少个矩形?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂采用甲、乙两种不同生产方式生产某零件,现对两种生产方式所生产的这种零件的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 100的为一等品;指标在区间
100的为一等品;指标在区间![]() 的为二等品
的为二等品![]() 现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
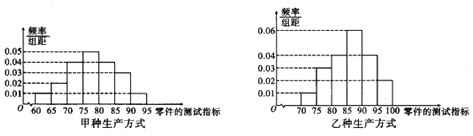
![]() 若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
![]() 将频率分布直方图中的频率视作概率,用样本估计总体
将频率分布直方图中的频率视作概率,用样本估计总体![]() 若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是
.下列结论正确的是

A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜加工厂加工一种蔬菜,并对该蔬菜产品进行质量评级,现对甲、乙两台机器所加工的蔬菜产品随机抽取一部分进行评级,结果(单位:件)如表1:

(1)若规定等级![]() 为合格等级,等级
为合格等级,等级![]() 为优良等级,能否有
为优良等级,能否有![]() 的把握认为“蔬菜产品加工质量与机器有关”?
的把握认为“蔬菜产品加工质量与机器有关”?
(2)表2是用清水![]() 千克清洗该蔬菜
千克清洗该蔬菜![]() 千克后,该蔬菜上残留的农药
千克后,该蔬菜上残留的农药![]() 微克的统计表,若用解析式
微克的统计表,若用解析式![]() 作为
作为![]() 与
与![]() 的回归方程,求出
的回归方程,求出![]() 与
与![]() 的回归方程.(结果精确到
的回归方程.(结果精确到![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com