
 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为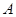 类工人),另外
类工人),另外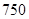 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按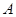 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查  名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).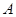 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?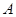 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.| 生产能力分组 |  |  |  |  |  |
| 人数 | 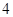 |  |  |  |  |
| 生产能力分组 |  |  |  |  |
| 人数 | 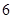 |  | 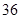 | 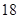 |


 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;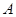 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组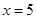 ,
,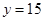 ;(2)详见解析;(3)
;(2)详见解析;(3)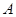 类工人、
类工人、 类工人以及该厂工人的生产能力的平均数分别为
类工人以及该厂工人的生产能力的平均数分别为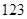 、
、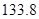 、
、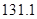 .
.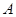 类工人和
类工人和 类工人中抽查的工人数;(2)①在(1)中的条件下,利用
类工人中抽查的工人数;(2)①在(1)中的条件下,利用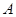 类工人和
类工人和 类工人所抽查的工人总数求出
类工人所抽查的工人总数求出 、
、 的值;②在频率分布直方图中,利用每组的区间的中点值乘以相应组的频率的乘积相加的方法求出
的值;②在频率分布直方图中,利用每组的区间的中点值乘以相应组的频率的乘积相加的方法求出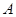 类工人和
类工人和 类工人的生产能力的平均数,然后再将
类工人的生产能力的平均数,然后再将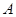 类工人和
类工人和 类工人生产能力平均数分别乘以
类工人生产能力平均数分别乘以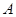 类工人和
类工人和 类工人的百分比的乘积相加的到该厂工人生产能力的平均数.
类工人的百分比的乘积相加的到该厂工人生产能力的平均数.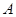 类工人和
类工人和 类工人中分别抽查
类工人中分别抽查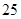 名和
名和 名;
名;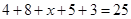 ,得
,得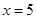 ,
,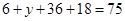 ,得
,得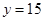 .频率分布直方图如下:
.频率分布直方图如下: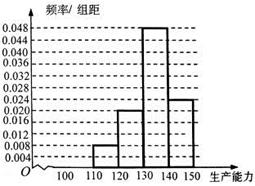
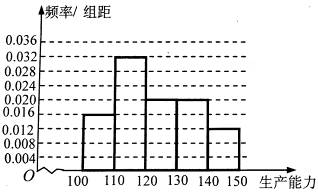
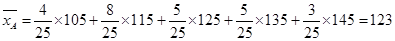 ,
, ,
,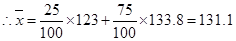 ,
,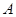 类工人生产能力的平均数,
类工人生产能力的平均数, 类工人生产能力的平均数以及该工厂工人生产能力的平均数的估计值分别为
类工人生产能力的平均数以及该工厂工人生产能力的平均数的估计值分别为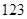 、
、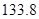 、
、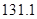 .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下: |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等. 与
与 的值;
的值; 件
件 种元件中任取
种元件中任取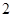 件,求
件,求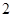 件都为正品的概率.
件都为正品的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 城市 | 民营企业数量 | 抽取数量 |
| A | 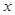 | 4 |
| B | 28 |  |
| C | 84 | 6 |
 、
、 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 智力评分 | 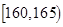 | 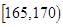 |  |  | 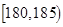 |  |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 智力评分 | 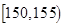 |  | 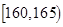 | 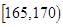 |  |  |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
零件数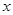 (个) (个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
加工时间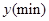 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 |
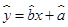 ,则点
,则点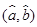 在直线
在直线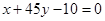 的( )
的( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| | 甲厂 | 乙厂 | 合计 |
| 优质品 | | | |
| 非优质品 | | | |
| 合 计 | | | |
| P(χ2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com