
【题目】已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值.
【答案】(1)a=4,b=4(2)单调增区间为(-∞,-2),![]() ;
;
单调减区间为![]() ,4-4e-2.
,4-4e-2.
【解析】(1)f′(x)=ex(ax+b)+aex-2x-4
=ex(ax+a+b)-2x-4,
∵y=f(x)在(0,f(0))处的切线方程为y=4x+4,
∴f′(0)=a+b-4=4,f(0)=b=4,
∴a=4,b=4.
(2)由(1)知f′(x)=4ex(x+2)-2(x+2)
=2(x+2)(2ex-1),
令f′(x)=0得x1=-2,x2=ln![]() ,
,
列表:
x | (-∞,-2) | -2 |
| ln |
|
f′(x) | + | 0 | - | 0 | + |
f(x) |
| 极大值 |
| 极小值 |
|
∴y=f(x)的单调增区间为(-∞,-2),![]() ;
;
单调减区间为![]() .
.
![]()
![]()
![]() f(x)极大值=f(-2)=4-4e-2.
f(x)极大值=f(-2)=4-4e-2.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sinxcosx+sin(x+
sinxcosx+sin(x+ ![]() )sin(x﹣
)sin(x﹣ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期和单调增区间;
(2)若x=x0(0≤x0≤ ![]() )为f(x)的一个零点,求cos2x0的值.
)为f(x)的一个零点,求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个人以6米/秒的匀速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始作变速直线行驶(汽车与人的前进方向相同),汽车在时刻t的速度为v(t)=t米/秒,那么,此人( )
A.可在7秒内追上汽车
B.可在9秒内追上汽车
C.不能追上汽车,但其间最近距离为14米
D.不能追上汽车,但其间最近距离为7米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asinB=﹣bsin(A+ ![]() ).
).
(1)求A;
(2)若△ABC的面积S= ![]() c2 , 求sinC的值.
c2 , 求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数y=f(x)的图象过点 ![]() .
.
(1)求函数f(x)的解析式
(2)记g(x)=f(x)+x , 判断g(x)在(1,+∞)上的单调性,并证明之.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
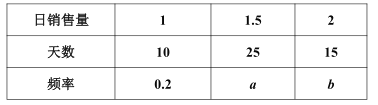
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元, ![]() 表示该种商品某两天销售利润的和(单位:千元),求
表示该种商品某两天销售利润的和(单位:千元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x>0时, ![]() .
.
(1)求f(x)的解析式;
(2)讨论函数f(x)的单调性,并求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com